Beschreibung
Anmerkung
Die Näherung von
a
2
{\displaystyle {\frac {a}{2}}}
K
L
¯
=
a
2
=
1
−
2
(
2
−
2
)
(
2
−
2
+
1
2
+
2
)
−
11
+
11
2
+
5
1
+
2
2
≈
r
⋅
0,886
226
932
777
110
[
L
E
]
{\displaystyle {\overline {KL}}={\frac {a}{2}}=1-{\frac {{\sqrt {2}}\left(2-{\sqrt {2}}\right)\left(2-{\sqrt {2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {2}}}}\right)}{-11+11{\sqrt {2}}+5{\sqrt {1+2{\sqrt {2}}}}}}\approx r\cdot \ 0{,}886\;226\;932\;777\;110\;[\mathrm {LE} ]}
Die Verwendung der Quadratwurzel aus 2 =
|
F
J
|
{\displaystyle |FJ|}
π
,
{\displaystyle \pi ,}
Konstruktion von Jakob de Gelder mit dem Zu Chongzhi-Bruch
355
113
{\displaystyle {\frac {355}{113}}}
Ergebnis der folgenden Konstruktion
3,141
592
705
…
{\displaystyle 3{,}141\;592\;{\color {red}\;705\;\ldots }}
Ergebnis mit Zu Chongzhi-Bruch
355
113
{\displaystyle {\frac {355}{113}}}
3.141
592
920
…
{\displaystyle 3.141\;592\;{\color {red}\;920\;\ldots }}
3,141
592
653
…
{\displaystyle 3{,}141\;592\;653\ldots }
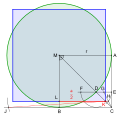
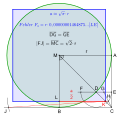
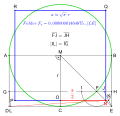
Konstruktion
Quadratur des Kreises, Näherungskonstruktion mithilfe
2
{\displaystyle {\sqrt {2}}}
Quadratur des Kreises, Näherungskonstruktion mithilfe
2
{\displaystyle {\sqrt {2}}}
Ziehe einen Kreis mit beliebigem Radius
r
{\displaystyle r}
M
.
{\displaystyle M.}
Zeichne das Quadrat
M
B
C
A
{\displaystyle MBCA}
r
{\displaystyle r}
C
B
¯
{\displaystyle {\overline {CB}}}
B
{\displaystyle B}
Ziehe die Diagonale
M
C
¯
,
{\displaystyle {\overline {MC}},}
D
.
{\displaystyle D.}
Zeichne eine Parallele zu
B
C
¯
{\displaystyle {\overline {BC}}}
D
{\displaystyle D}
A
C
¯
,
{\displaystyle {\overline {AC}},}
E
.
{\displaystyle E.}
Ziehe einen Halbkreis um
D
{\displaystyle D}
E
{\displaystyle E}
F
.
{\displaystyle F.}
Halbiere die Strecke
D
E
¯
{\displaystyle {\overline {DE}}}
G
.
{\displaystyle G.}
Verbinde
G
{\displaystyle G}
C
,
{\displaystyle C,}
H
.
{\displaystyle H.}
Bestimme den Punkt
J
{\displaystyle J}
|
F
J
|
=
M
C
¯
=
2
⋅
r
.
{\displaystyle |FJ|={\overline {MC}}={\sqrt {2}}\cdot r.}
Verbinde
J
{\displaystyle J}
H
{\displaystyle H}
K
.
{\displaystyle K.}
Zeichne eine Parallele zu
B
C
¯
{\displaystyle {\overline {BC}}}
K
{\displaystyle K}
M
B
¯
,
{\displaystyle {\overline {MB}},}
L
.
{\displaystyle L.}
Wird die Strecke
K
L
¯
{\displaystyle {\overline {KL}}}
a
{\displaystyle a}
Fehler
Bei einem Kreis mit Radius r = 1 [LE]:
Konstruierte Seite des Quadrates a = 1,772453865554221... [LE]
Soll-Seite des Quadrates a s =
π
⋅
1
[
L
E
]
{\displaystyle {\sqrt {\pi }}\cdot 1[LE]}
Absoluter Fehler = a - a s = 0,000000014648705... = 1,4648...E-8 [LE]
Fläche des konstruierten Quadrates A = a 2 = 3,141592705518100... [FE]
Soll-Fläche des Quadrates A s =
π
⋅
1
[
F
E
]
{\displaystyle {\pi }\cdot 1[FE]}
Absoluter Fehler = A - A s = 0,000000051928307... = 5,1928...E-8 [FE]
Fazit: Sieben Nachkommastellen sind gleich denen von
π
{\displaystyle {\sqrt {\pi }}}
π
{\displaystyle \pi }
Bei einem Kreis mit dem Radius r = 100 km wäre der Fehler der Seite a ≈ 1,5 mm
Bei einem Kreis mit dem Radius r = 10 m wäre der Fehler der Fläche A ≈ 5,2 mm2
Annotation
The approximation of
a
2
{\displaystyle {\frac {a}{2}}}
K
L
¯
=
a
2
=
1
−
2
(
2
−
2
)
(
2
−
2
+
1
2
+
2
)
−
11
+
11
2
+
5
1
+
2
2
≈
r
⋅
0.886
226
932
777
110
[
u
l
]
{\displaystyle {\overline {KL}}={\frac {a}{2}}=1-{\frac {{\sqrt {2}}\left(2-{\sqrt {2}}\right)\left(2-{\sqrt {2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {2}}}}\right)}{-11+11{\sqrt {2}}+5{\sqrt {1+2{\sqrt {2}}}}}}\approx r\cdot \ 0.886\;226\;932\;777\;110\;[\mathrm {ul} ]}
The use of the square root of 2 =
|
F
J
|
{\displaystyle |FJ|}
π
,
{\displaystyle \pi ,}
construction by Jakob de Gelder with the Zu Chongzhi fraction
355
113
.
{\displaystyle {\frac {355}{113}}.}
Result of the following construction
3.141
592
705
…
{\displaystyle 3.141\;592\;{\color {red}\;705\;\ldots }}
Result with Zu Chongzhi fraction
355
113
{\displaystyle {\frac {355}{113}}}
3.141
592
920
…
{\displaystyle 3.141\;592\;{\color {red}\;920\;\ldots }}
3.141
592
653
…
{\displaystyle 3.141\;592\;653\ldots }
Construction
Squaring the circle, approximate construction with help
2
{\displaystyle {\sqrt {2}}}
Squaring the circle, approximate construction with help
2
{\displaystyle {\sqrt {2}}}
Draw a circle with any radius
r
{\displaystyle r}
M
.
{\displaystyle M.}
Draw the square
M
B
C
A
{\displaystyle MBCA}
r
{\displaystyle r}
C
B
¯
{\displaystyle {\overline {CB}}}
B
.
{\displaystyle B.}
Draw the diagonal
M
C
¯
,
{\displaystyle {\overline {MC}},}
D
.
{\displaystyle D.}
Draw a parallel to
B
C
¯
{\displaystyle {\overline {BC}}}
D
{\displaystyle D}
A
C
¯
,
{\displaystyle {\overline {AC}},}
E
.
{\displaystyle E.}
Draw a semicircle around
D
{\displaystyle D}
F
.
{\displaystyle F.}
Halve the line segment
D
E
¯
{\displaystyle {\overline {DE}}}
G
.
{\displaystyle G.}
Connect
G
{\displaystyle G}
C
,
{\displaystyle C,}
H
.
{\displaystyle H.}
Find the point
J
{\displaystyle J}
|
F
J
|
=
M
C
¯
=
2
⋅
r
.
{\displaystyle |FJ|={\overline {MC}}={\sqrt {2}}\cdot r.}
Connect
J
{\displaystyle J}
H
,
{\displaystyle H,}
K
.
{\displaystyle K.}
Draw a parallel to
B
C
¯
{\displaystyle {\overline {BC}}}
K
{\displaystyle K}
M
B
¯
,
{\displaystyle {\overline {MB}},}
L
.
{\displaystyle L.}
If the line segment
K
L
¯
{\displaystyle {\overline {KL}}}
a
{\displaystyle a}
Error
In a circle of radius r = 1 [unit length, ul]:
Constructed side of the square a = 1.772453865554221... [
u
l
{\displaystyle ul}
Target side of the square a s =
π
⋅
1
[
u
l
]
{\displaystyle {\sqrt {\pi }}\cdot 1[ul]}
u
l
{\displaystyle ul}
Absolute error = a - a s = 0.000000014648705... = 1.4648...E-8 [
u
l
{\displaystyle ul}
Surface of the constructed square A = a 2 = 3.141592705518100... [unit area, ua]
Target area of the square A s =
π
⋅
1
[
u
a
]
{\displaystyle {\pi }\cdot 1[ua]}
u
a
{\displaystyle ua}
Absolute error = A - A s = 0.000000051928307... = 5.1928...E-8 [
u
a
{\displaystyle ua}
Conclusion: seven decimal places are equal to those of
π
{\displaystyle {\sqrt {\pi }}}
π
{\displaystyle \pi }
In a circle of radius r = 100 km would be the fault of the page a ≈ 1.5 mm
In the case of a circle with the radius r = 10 m would be the error of the surface A ≈ 5.2 mm2
Lizenz
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
Dieses Werk darf von dir
verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werdenneu zusammengestellt werden – abgewandelt und bearbeitet werden
Zu den folgenden Bedingungen:
Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten. https://creativecommons.org/licenses/by-sa/4.0 CC BY-SA 4.0 Creative Commons Attribution-Share Alike 4.0 true true Deutsch Ergänze eine einzeilige Erklärung, was diese Datei darstellt.










![{\displaystyle {\overline {KL}}={\frac {a}{2}}=1-{\frac {{\sqrt {2}}\left(2-{\sqrt {2}}\right)\left(2-{\sqrt {2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {2}}}}\right)}{-11+11{\sqrt {2}}+5{\sqrt {1+2{\sqrt {2}}}}}}\approx r\cdot \ 0{,}886\;226\;932\;777\;110\;[\mathrm {LE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da96da4ffd59dc73ae1e96655d160ac14772adf6)




































![{\displaystyle {\sqrt {\pi }}\cdot 1[LE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/756d2a81fbab81e23a5fddaf269cd105f78f7b59)
![{\displaystyle {\pi }\cdot 1[FE]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8229175d34d3772c21f8878f274781dbd03fb53e)

![{\displaystyle {\overline {KL}}={\frac {a}{2}}=1-{\frac {{\sqrt {2}}\left(2-{\sqrt {2}}\right)\left(2-{\sqrt {2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {2}}}}\right)}{-11+11{\sqrt {2}}+5{\sqrt {1+2{\sqrt {2}}}}}}\approx r\cdot \ 0.886\;226\;932\;777\;110\;[\mathrm {ul} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e227646be0d1a7d383909880453b35c75254fb4)






![{\displaystyle {\sqrt {\pi }}\cdot 1[ul]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcb063aa5c3bce6b8b5f03a11d8778acec6b460d)
![{\displaystyle {\pi }\cdot 1[ua]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/613e595ca322831756972cea9b0f0108b13621c1)
