| Die Beschreibung dieser Datei stellt nicht genügend Informationen zur Verfügung, um einer breiten Leserschaft zu ermöglichen, den Gegenstand zu identifizieren.
Bitte ergänze weitere Details in der Beschreibung, so dass Leser mindestens in einer Hauptsprache den Gegenstand identifizieren können. (Aus dieser können dann andere weitere Übersetzungen erstellen.) Eine englische Beschreibung sollte möglichst hinzugefügt werden.
Deutsch | English | español | français | 日本語 | македонски | മലയാളം | português | +/− |
Beschreibung

|
Dieses Bild des Typs Math sollte als Vektorgrafik im SVG-Format neu erstellt werden. Vektorformate haben zahlreiche Vorteile; weitere Information unter Commons:Media for cleanup. Wenn dir eine SVG-Version dieses Bildes vorliegt, so lade diese bitte hoch. Nach dem Hochladen der Datei ist diese Vorlage auf der aktuellen Bildbeschreibungsseite durch die Vorlage {{Vector version available}}, oder kürzer {{Vva}}, zu ersetzen. Es ist empfohlen die neue SVG-Datei „Discontinuity removable.eps.svg“ zu nennen – dann benötigt die Vorlage vector version available (bzw. vva) keinen Parameter. |
Source code:
function discontinuity()
% set up the plotting window
thick_line=2.5; thin_line=2; arrow_size=14; arrow_type=2;
fs=30; circrad=0.06;
% picture 1
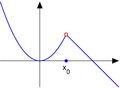
a=-1.5; b=3; h=0.02; x0=1;
X1=a:h:x0; X2=x0:h:b; X=[X1 X2];
Y1=X1.^2; Y2=Y1(length(Y1))+(-1)*(X2-X2(1)); Y=[Y1 Y2]; y01=Y1(length(Y1)); y02=Y2(1);
figure(1); clf; hold on; axis equal; axis off;
axes_points(a, b, thin_line, thick_line, arrow_size, arrow_type, x0, y01, y02, circrad, fs, X, Y, X1, Y1, X2, Y2)
saveas(gcf, 'discontinuity_removable.eps', 'psc2')
% picture 2
a=-1.5; b=3; h=0.02; x0=1;
X1=a:h:x0; X2=x0:h:b; X=[X1 X2];
Y1=X1.^2; Y2=2-(X2-x0).^2; Y=[Y1 Y2]; y01=Y1(length(Y1)); y02=Y2(1);
figure(2); clf; hold on; axis equal; axis off;
axes_points(a, b, thin_line, thick_line, arrow_size, arrow_type, x0, y01, y02, circrad, fs, X, Y, X1, Y1, X2, Y2)
saveas(gcf, 'discontinuity_jump.eps', 'psc2')
% picture 3
a=-1.5; b=3; h=0.001; x0=1;
X1=a:h:x0; X2=x0:h:b; X=[X1 X2];
Y1=sin(5./(X1-x0-eps)); Y2=0.1./(X2-x0+50*h); Y=[Y1 Y2]; y01=Y1(length(Y1)); y02=Y2(1);
figure(3); clf; hold on; axis equal; axis off;
axes_points2(a, b, thin_line, thick_line, arrow_size, arrow_type, x0, NaN, NaN, circrad, fs, X, Y, X1, Y1, X2, Y2)
saveas(gcf, 'discontinuity_essential.eps', 'psc2')
disp('Converting to png...')
! convert -density 400 -antialias discontinuity_removable.eps discontinuity_removable.png
! convert -density 400 -antialias discontinuity_jump.eps discontinuity_jump.png
! convert -density 400 -antialias discontinuity_essential.eps discontinuity_essential.png
function axes_points(a, b, thin_line, thick_line, arrow_size, arrow_type, x0, y01, y02, circrad, fs, X, Y, X1, Y1, X2, Y2)
arrow([a 0], [b, 0], thin_line, arrow_size, pi/8,arrow_type, [0, 0, 0]) % xaxis
small=0.2; arrow([0, min(Y)], [0, max(Y)], thin_line, arrow_size, pi/8,arrow_type, [0, 0, 0]); % y axis
plot(X1, Y1, 'linewidth', thick_line); plot(X2, Y2, 'linewidth', thick_line)
ball(x0, 0, circrad, [0 0 1 ]);
ball_empty(x0, y01, thick_line, circrad, [1 0 0 ]); ball_empty(x0, y02, thick_line, circrad, [1 0 0 ]);
H=text(x0, -0.006*fs, 'x_0'); set(H, 'fontsize', fs, 'HorizontalAlignment', 'c', 'VerticalAlignment', 'c')
function axes_points2(a, b, thin_line, thick_line, arrow_size, arrow_type, x0, y01, y02, circrad, fs, X, Y, X1, Y1, X2, Y2)
arrow([a 0], [b, 0], thin_line, arrow_size, pi/8,arrow_type, [0, 0, 0]) % xaxis
small=0.2; arrow([0, min(Y)], [0, max(Y)], thin_line, arrow_size, pi/8,arrow_type, [0, 0, 0]); % y axis
plot(X1, Y1, 'linewidth', thick_line); plot(X2, Y2, 'linewidth', thick_line)
ball(x0, 0, circrad, [0 0 1 ]);
ball_empty(x0, y01, thick_line, circrad, [1 0 0 ]); ball_empty(x0, y02, thick_line, circrad, [1 0 0 ]);
H=text(x0+0.2, -0.006*fs, 'x_0'); set(H, 'fontsize', fs, 'HorizontalAlignment', 'c', 'VerticalAlignment', 'c')
function ball(x, y, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, color);
set(H, 'EdgeColor', 'none');
function ball_empty(x, y, thick_line, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, [1 1 1]);
%set(H, 'EdgeColor', color);
plot(X, Y, 'color', color, 'linewidth', thick_line);
function arrow(start, stop, thickness, arrowsize, sharpness, arrow_type, color)
% draw a line with an arrow at the end
% start is the x,y point where the line starts
% stop is the x,y point where the line stops
% thickness is an optional parameter giving the thickness of the lines
% arrowsize is an optional argument that will give the size of the arrow
% It is assumed that the axis limits are already set
% 0 < sharpness < pi/4 determines how sharp to make the arrow
% arrow_type draws the arrow in different styles. Values are 0, 1, 2, 3.
% 8/4/93 Jeffery Faneuff
% Copyright (c) 1988-93 by the MathWorks, Inc.
% Modified by Oleg Alexandrov 2/16/03
if nargin <=6
color=[0, 0, 0];
end
if (nargin <=5)
arrow_type=0; % the default arrow, it looks like this: ->
end
if (nargin <=4)
sharpness=pi/4; % the arrow sharpness - default = pi/4
end
if nargin<=3
xl = get(gca,'xlim');
yl = get(gca,'ylim');
xd = xl(2)-xl(1);
yd = yl(2)-yl(1);
arrowsize = (xd + yd) / 2; % this sets the default arrow size
end
if (nargin<=2)
thickness=0.5; % default thickness
end
xdif = stop(1) - start(1);
ydif = stop(2) - start(2);
if (xdif == 0)
if (ydif >0)
theta=pi/2;
else
theta=-pi/2;
end
else
theta = atan(ydif/xdif); % the angle has to point according to the slope
end
if(xdif>=0)
arrowsize = -arrowsize;
end
if (arrow_type == 0) % draw the arrow like two sticks originating from its vertex
xx = [start(1), stop(1),(stop(1)+0.02*arrowsize*cos(theta+sharpness)),NaN,stop(1),...
(stop(1)+0.02*arrowsize*cos(theta-sharpness))];
yy = [start(2), stop(2), (stop(2)+0.02*arrowsize*sin(theta+sharpness)),NaN,stop(2),...
(stop(2)+0.02*arrowsize*sin(theta-sharpness))];
plot(xx,yy, 'LineWidth', thickness, 'color', color)
end
if (arrow_type == 1) % draw the arrow like an empty triangle
xx = [stop(1),(stop(1)+0.02*arrowsize*cos(theta+sharpness)), ...
stop(1)+0.02*arrowsize*cos(theta-sharpness)];
xx=[xx xx(1) xx(2)];
yy = [stop(2),(stop(2)+0.02*arrowsize*sin(theta+sharpness)), ...
stop(2)+0.02*arrowsize*sin(theta-sharpness)];
yy=[yy yy(1) yy(2)];
plot(xx,yy, 'LineWidth', thickness, 'color', color)
% plot the arrow stick
plot([start(1) stop(1)+0.02*arrowsize*cos(theta)*cos(sharpness)], [start(2), stop(2)+ ...
0.02*arrowsize*sin(theta)*cos(sharpness)], 'LineWidth', thickness, 'color', color)
end
if (arrow_type==2) % draw the arrow like a full triangle
xx = [stop(1),(stop(1)+0.02*arrowsize*cos(theta+sharpness)), ...
stop(1)+0.02*arrowsize*cos(theta-sharpness),stop(1)];
yy = [stop(2),(stop(2)+0.02*arrowsize*sin(theta+sharpness)), ...
stop(2)+0.02*arrowsize*sin(theta-sharpness),stop(2)];
H=fill(xx, yy, color);% fill with black
set(H, 'EdgeColor', 'none')
% plot the arrow stick
plot([start(1) stop(1)+0.01*arrowsize*cos(theta)], [start(2), stop(2)+ ...
0.01*arrowsize*sin(theta)], 'LineWidth', thickness, 'color', color)
end
if (arrow_type==3) % draw the arrow like a filled 'curvilinear' triangle
curvature=0.5; % change here to make the curved part more curved (or less curved)
radius=0.02*arrowsize*max(curvature, tan(sharpness));
x1=stop(1)+0.02*arrowsize*cos(theta+sharpness);
y1=stop(2)+0.02*arrowsize*sin(theta+sharpness);
x2=stop(1)+0.02*arrowsize*cos(theta)*cos(sharpness);
y2=stop(2)+0.02*arrowsize*sin(theta)*cos(sharpness);
d1=sqrt((x1-x2)^2+(y1-y2)^2);
d2=sqrt(radius^2-d1^2);
d3=sqrt((stop(1)-x2)^2+(stop(2)-y2)^2);
center(1)=stop(1)+(d2+d3)*cos(theta);
center(2)=stop(2)+(d2+d3)*sin(theta);
alpha=atan(d1/d2);
Alpha=-alpha:0.05:alpha;
xx=center(1)-radius*cos(Alpha+theta);
yy=center(2)-radius*sin(Alpha+theta);
xx=[xx stop(1) xx(1)];
yy=[yy stop(2) yy(1)];
H=fill(xx, yy, color);% fill with black
set(H, 'EdgeColor', 'none')
% plot the arrow stick
plot([start(1) center(1)-radius*cos(theta)], [start(2), center(2)- ...
radius*sin(theta)], 'LineWidth', thickness, 'color', color);
end
Übertragen aus en.wikipedia nach Commons durch Maksim.
Die ursprüngliche Dateibeschreibungsseite war
removable.eps.png hier. Alle folgenden Benutzernamen beziehen sich auf en.wikipedia.
| date/time |
username |
edit summary
|
| 03:11, 14 September 2005 |
en:User:Oleg Alexandrov |
(<span class="autocomment"><a href="/wiki/Image:Discontinuity_removable.eps.png#Licensing" title="Image:Discontinuity removable.eps.png">→</a>Licensing</span>)
|
| 00:51, 12 September 2005 |
en:User:Oleg Alexandrov |
(Made by me with matlab. )
|
Ursprüngliches Datei-Logbuch
Legend: (cur) = this is the current file, (del) = delete this old version, (rev) = revert to this old version.
Click on date to download the file or see the image uploaded on that date.
Lizenz
| Public domainPublic domainfalsefalse
|

|
Dieses Diagramm ist gemeinfrei („public domain“), weil es nur Allgemeingut enthält und die nötige Schöpfungshöhe nicht erreicht.
|