\documentclass[border=10pt]{standalone}

\usepackage[utf8]{inputenc}
\usepackage{amsmath}
\usepackage{amssymb}

\usepackage{tikz}
\usetikzlibrary{shapes,arrows}

\everymath{\displaystyle}

\begin{document}
\tikzstyle{decision} = [diamond, draw, fill=yellow!20,
  aspect=2, text badly centered, inner sep=0pt]

\tikzstyle{block} = [rectangle, draw, fill=blue!20,
  text centered, rounded corners]

\tikzstyle{convergence} = [rectangle, draw, fill=green!20,
  node distance=8cm, text centered, rounded corners]

\tikzstyle{divergence} = [rectangle, draw, fill=red!20,
  node distance=8cm, text centered, rounded corners]

  \tikzstyle{line} = [-stealth, thick, draw]

\begin{tikzpicture}[node distance=4cm, auto, text width=12em]
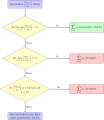
  \node [block] (init) {Quotienten $\left|\frac{a_{k+1}}{a_k}\right|$ bilden};
  \node [decision, below of=init, node distance=3cm] (case1) {Ist $\limsup_{k\to\infty} \left|\frac{a_{k+1}}{a_k}\right| < 1$?};
  \node [decision, below of=case1] (case2) {Ist $\liminf_{k\to\infty} \left|\frac{a_{k+1}}{a_k}\right| > 1$?};
  \node [decision, below of=case2] (case3) {Ist $\left|\frac{a_{k+1}}{a_k}\right| \ge 1$ für fast alle $k\in\mathbb N$?};
  \node [convergence, right of=case1] (yes1) {$\sum_{k=1}^\infty a_k$ konvergiert absolut};
  \node [divergence, right of=case2] (no2) {$\sum_{k=1}^\infty a_k$ divergiert};
  \node [divergence, right of=case3] (no3) {$\sum_{k=1}^\infty a_k$ divergiert};
  \node [block, below of=case3, node distance=3.5cm] (final) {Quotientenkriterium kann nicht angewendet werden};
  \path [line] (init) edge (case1);
  \path [line] (case1) -- node [xshift=5em] {Ja} (yes1);
  \path [line] (case2) -- node [xshift=5em] {Ja} (no2);
  \path [line] (case3) -- node [xshift=5em] {Ja} (no3);
  \path [line] (case1) -- node {Nein} (case2);
  \path [line] (case2) -- node {Nein} (case3);
  \path [line] (case3) -- node {Nein} (final);
\end{tikzpicture}

\end{document}