Datei:Illustration CRPS.png
Illustration_CRPS.png (547 × 432 Pixel, Dateigröße: 18 KB, MIME-Typ: image/png)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Beschreibung
| BeschreibungIllustration CRPS.png |
English: Illustration of the continous ranked probability score (CRPS). Given a sample y and a predicted cumulative distribution F, the CRPS is given by computing the difference between the curves at each point x of the support, squaring it and integrating it over the whole support.
Deutsch: Illustration des kontinuierlichen Rang-Wahrscheinlichkeits-Scores (CRPS). Gegeben ist eine Stichprobe y und eine vorhergesagte kumulative Verteilung F. Der CRPS wird berechnet, indem man die Differenz zwischen den Kurven an jedem Punkt x des Trägers berechnet, diese Differenz quadriert und über den gesamten Träger integriert. |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Biggerj1 |
import matplotlib.pyplot as plt
import numpy as np
# Define the step function
def step_function(x):
return 0 if x < 0 else 1
# Define the sigmoid function
def sigmoid_function(x):
return 1 / (1 + np.exp(-x))
# Generate x values
x_high_res = np.linspace(-10, 10, 1000) # High resolution for the functions
x_low_res = np.linspace(-10, 10, 71) # Low resolution for the bars
# Calculate y values for both functions
y_step = [step_function(i) for i in x_high_res]
y_sigmoid = [sigmoid_function(i) for i in x_high_res]
# Plot both functions
plt.plot(x_high_res, y_step, label=r'$\mathbb{1}_{x>y}$')
plt.plot(x_high_res, y_sigmoid, label='F')
# Create a series of vertical bars to represent the area between the two functions
for i in range(len(x_low_res) - 1):
bar_height = abs(sigmoid_function(x_low_res[i]) - step_function(x_low_res[i]))
bar_width = x_low_res[i+1]-x_low_res[i] if i != len(x_low_res) - 2 else x_low_res[-1]-x_low_res[-2]
plt.bar(x_low_res[i], bar_height, bottom=min(step_function(x_low_res[i]), sigmoid_function(x_low_res[i])), width=bar_width, color='grey', align='edge', alpha=0.5)
# Add an annotation for the grey area
plt.annotate('CRPS', xy=(0.75, 0.75), xytext=(-3, 0.7),
arrowprops=dict(facecolor='black', shrink=0.05))
# Add labels and title
plt.xlabel('x')
#plt.title('Step Function vs Sigmoid Function')
plt.legend()
# Display the plot
plt.show()
Lizenz
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
Diese Datei ist lizenziert unter der Creative-Commons-Lizenz „Namensnennung – Weitergabe unter gleichen Bedingungen 4.0 international“.
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
Ergänze eine einzeilige Erklärung, was diese Datei darstellt.
Illustration of the continous ranked probability score (CRPS).
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
4. September 2023
image/png
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 21:00, 4. Sep. 2023 | 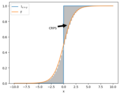 | 547 × 432 (18 KB) | Biggerj1 | Uploaded own work with UploadWizard |
Dateiverwendung
Die folgende Seite verwendet diese Datei:
Globale Dateiverwendung
Die nachfolgenden anderen Wikis verwenden diese Datei:
- Verwendung auf en.wikipedia.org
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| Software |
|
|---|---|
| Horizontale Auflösung | 39,37 dpc |
| Vertikale Auflösung | 39,37 dpc |
Abgerufen von „https://de.wikipedia.org/wiki/Datei:Illustration_CRPS.png“
