Datei:Poincare-sphere arrows.svg

Größe der PNG-Vorschau dieser SVG-Datei: 600 × 600 Pixel. Weitere aus SVG automatisch erzeugte PNG-Grafiken in verschiedenen Auflösungen: 240 × 240 Pixel | 480 × 480 Pixel | 768 × 768 Pixel | 1.024 × 1.024 Pixel | 2.048 × 2.048 Pixel

Originaldatei (SVG-Datei, Basisgröße: 600 × 600 Pixel, Dateigröße: 6 KB)

Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.

Zur Beschreibungsseite auf Commons

Beschreibung

BeschreibungPoincare-sphere arrows.svg	English: Drawing of a Poincaré sphere, which illustrates the space of possible polarisations of electromagnetic waves. The sphere is drawn with three great circles, labels for six basic polarisations H (linear horizontal), V (linear vertical), D (linear diagonal), A (linear antidiagonal), R (right-hand circular) and L (left-hand circular) and images of the polarisation vectors for each. Additionally the coordinate system of Stokes vectors with components S₁, S₂ and S₃ is drawn in the center of the sphere. Deutsch: Zeichnung einer Poincaré-Kugel, die den Raum der möglichen Polarisationen elektromagnetischer Wellen darstellt. Die Kugel ist mit drei Großkreisen gezeichnet, Zeichen für die sechs Basispolarisationen H (linear horizontal), V (linear vertikal), D (linear diagonal), A (linear antidiagonal), R (rechtshändig zirkular) and L (linkshändig zirkular) und mit Bildern der Polarisationsvektoren für jede davon. Zusätzlich befindet sich im Zentrum der Kugel das Koordinatensystem aus Stokesvektorkomponenten S₁, S₂ and S₃.
Datum	31. August 2014
Quelle	Eigenes Werk
Urheber	Geek3
Andere Versionen	Poincare-sphere_stokes.svg (without the small images of the polarisation vectors)

Source Code

The image is created by the following source-code. Requirements:

python source code:

try:
    import svgwrite as svg
except ImportError:
    print 'You need to install svgwrite: http://pypi.python.org/pypi/svgwrite/'
    # documentation at http://pythonhosted.org/svgwrite/
    exit(1)

from math import *

def to_xyz(theta, phi, r=1):
    return r * sin(theta) * cos(phi), r * sin(theta) * sin(phi), r * cos(theta)

def to_theta_phi_r(x, y, z):
    return atan2(z, sqrt(x**2 + y**2)), atan2(x, y), sqrt(x**2+y**2+z**2)
    
def rotx(x, y, z, a):
    y, z = cos(a) * y + sin(a) * z, cos(a) * z - sin(a) * y
    return x, y, z

def ellipse_path(theta, phi, tilt, flip=False):
    t, p, r2 = to_theta_phi_r(*rotx(*(to_xyz(theta, phi, 1) + (tilt,))))
    a = abs(r)
    b = abs(r * sin(t))
    return 'M %f,%f A %f,%f %f %i,%i %f,%f' % (-r*cos(p), -r*sin(p),
        a, b, p*180/pi, 0, {True:1, False:0}[flip], r*cos(p), r*sin(p))

# document
size = 600, 600
doc = svg.Drawing('poincare-sphere_arrows.svg', profile='full', size=size)
doc.set_desc('poincare-sphere_arrows.svg', '''Drawing of a poincare-sphere with polarisations H, V, D, A, R and L, a coordinate system of Stokes-Vectors P1, P2 and P3 and six little images that illustrate the polarisations
rights: GNU Free Documentation license,
        Creative Commons Attribution ShareAlike license''')

# settings
dash = '8,6'
col = 'black'
r = 240
tilt = radians(-70)
phi = radians(-25)
cp, sp = cos(phi), sin(phi)

# background
doc.add(doc.rect(id='background', profile='full', insert=(0, 0), size=size, fill='white', stroke='none'))

# arrow markers
arrow_d = 'M -4,0 L 2,-3 L 1,0 L 2,3 L -4,0 z'
arrow1 = doc.marker(id='arrow1', orient='auto', overflow='visible')
arrow1.add(doc.path(d=arrow_d, fill=col, stroke='none',
    transform='rotate(180) scale(0.7)'))
doc.defs.add(arrow1)
arrow2 = doc.marker(id='arrow2', orient='auto', overflow='visible')
arrow2.add(doc.path(d=arrow_d, fill=col, stroke='none',
    transform='scale(0.7)'))
doc.defs.add(arrow2)
arrow3 = doc.marker(id='arrow3', orient='auto', overflow='visible')
arrow3.add(doc.path(d='M 8.7185878,4.0337352 L -2.2072895,0.016013256 L 8.7185884,-4.0017078 C 6.9730900,-1.6296469 6.9831476,1.6157441 8.7185878,4.0337352 z', fill=col, stroke='none',
    transform='scale(0.8) rotate(180)'))
doc.defs.add(arrow3)

# make a group for the sphere
sphere = doc.g(transform='translate(300, 300)', fill='none', stroke=col, stroke_width='2')
sphere['font-family'] = 'DejaVu Sans'
sphere['font-size'] = '42px'
doc.add(sphere)

# back ellipses
sphere.add(doc.path(d=ellipse_path(0, 0, tilt),
    stroke_dasharray=dash, stroke=col))
sphere.add(doc.path(d=ellipse_path(pi/2, phi, tilt, True),
    stroke_dasharray=dash, stroke=col))
sphere.add(doc.path(d=ellipse_path(pi/2, phi+pi/2, tilt),
    stroke_dasharray=dash, stroke=col))

# draw coordinate axes
sphere.add(doc.circle(center=(0, 0), r=5, fill=col, stroke='none'))
for i in range(3):
    xyz = [0, 0, 0]
    xyz[i] = 0.3 * r
    x, y, z = xyz
    x, y, z = rotx(x*cp + y*sp, y*cp - x*sp, z, tilt)
    line = doc.line(start=(0, 0), end=('%f' % x, '%f' % y), stroke=col)
    line['marker-end'] = arrow3.get_funciri()
    sphere.add(line)

# the six defined points
pts = []
for x,y,z in [[0,0,-1], [0,0,1], [0,-1,0], [0,1,0], [-1,0,0], [1,0,0]]:
    x, y, z = rotx(r * (x*cp + y*sp), r * (y*cp - x*sp), r * z, tilt)
    if z >= 0:
        continue
    pts.append((x, y))
    sphere.add(doc.circle(center=('%f' % x, '%f' % y), r=6,
        fill=col, stroke='none'))

# inset images
rect = doc.rect((-22, -22), (44, 44), fill='white', stroke=col, fill_opacity=0.88)

gV = doc.g(transform='translate(%f, %f)' % pts[1])
gV.add(rect)
gV.add(doc.line(start=(0,-11), end=(0,11), stroke_width=3,
    marker_end=arrow1.get_funciri(), marker_start=arrow2.get_funciri()))
sphere.add(gV)

gA = doc.g(transform='translate(%f, %f)' % pts[2])
gA.add(rect)
gA.add(doc.line(start=(-7,-7), end=(7,7), stroke_width=3,
    marker_end=arrow1.get_funciri(), marker_start=arrow2.get_funciri()))
sphere.add(gA)

gL = doc.g(transform='translate(%f, %f)' % pts[0])
gL.add(rect)
gL.add(doc.path(d='M -12,0 A 12,12 0 1,0 0,-12', stroke_width=3,
    marker_end=arrow1.get_funciri()))
sphere.add(gL)

# V label
sphere.add(doc.text('V', text_anchor='middle',
    transform='translate(144, -86)', stroke='none', fill=col))

# Stokes-Vector labels
sphere.add(doc.text('S₁', text_anchor='middle',
    transform='translate(-56, 33)', stroke='none', fill=col))
sphere.add(doc.text('S₂', text_anchor='middle',
    transform='translate(63, -2)', stroke='none', fill=col))
sphere.add(doc.text('S₃', text_anchor='middle',
    transform='translate(-29, -59)', stroke='none', fill=col))

# sphere surface
grad1 = doc.defs.add(doc.radialGradient(id='grad1',
    center=(0.375, 0.15), r=0.75, gradientUnits='objectBoundingBox'))
grad1.add_stop_color(offset=0, color='#ffffff', opacity=0.3)
grad1.add_stop_color(offset=1, color='#dddddd', opacity=0.3)
sphere.add(doc.circle(center=(0, 0), r=str(r),
    fill='url(#grad1)', stroke='none'))
grad2 = doc.defs.add(doc.radialGradient(id='grad2',
    center=(0.45, 0.45), r=0.575, gradientUnits='objectBoundingBox'))
grad2.add_stop_color(offset=0.6, color='#cccccc', opacity=0)
grad2.add_stop_color(offset=0.8, color='#cccccc', opacity=0.2)
grad2.add_stop_color(offset=1, color='#333333', opacity=0.2)
sphere.add(doc.circle(center=(0, 0), r=str(r),
    fill='url(#grad2)', stroke='none'))

# the six defined points
for x,y,z in [[0,0,-1], [0,0,1], [0,-1,0], [0,1,0], [-1,0,0], [1,0,0]]:
    x, y, z = rotx(r * (x*cp + y*sp), r * (y*cp - x*sp), r * z, tilt)
    if z < 0:
        continue
    pts.append((x, y))
    sphere.add(doc.circle(center=('%f' % x, '%f' % y), r=6,
        fill=col, stroke='none'))

# H, D, A, R, L labels
sphere.add(doc.text('H', text_anchor='middle',
    transform='translate(-144, 115)', stroke='none', fill=col))
sphere.add(doc.text('D', text_anchor='middle',
    transform='translate(272, 52)', stroke='none', fill=col))
sphere.add(doc.text('A', text_anchor='middle',
    transform='translate(-272, -26)', stroke='none', fill=col))
sphere.add(doc.text('R', text_anchor='middle',
    transform='translate(0, -261)', stroke='none', fill=col))
sphere.add(doc.text('L', text_anchor='middle',
    transform='translate(0, 291)', stroke='none', fill=col))

# front ellipses
sphere.add(doc.path(d=ellipse_path(0, 0, tilt, True)))
sphere.add(doc.path(d=ellipse_path(pi/2, phi, tilt)))
sphere.add(doc.path(d=ellipse_path(pi/2, phi+pi/2, tilt, True)))

# circle edge
sphere.add(doc.circle(center=(0, 0), r=str(r)))

# inset images
gH = doc.g(transform='translate(%f, %f)' % pts[4])
gH.add(rect)
gH.add(doc.line(start=(-11,0), end=(11,0), stroke_width=3,
    marker_end=arrow1.get_funciri(), marker_start=arrow2.get_funciri()))
sphere.add(gH)

gD = doc.g(transform='translate(%f, %f)' % pts[5])
gD.add(rect)
gD.add(doc.line(start=(-7,7), end=(7,-7), stroke_width=3,
    marker_end=arrow1.get_funciri(), marker_start=arrow2.get_funciri()))
sphere.add(gD)

gR = doc.g(transform='translate(%f, %f)' % pts[3])
gR.add(rect)
gR.add(doc.path(d='M 12,0 A 12,12 0 1,1 0,-12', stroke_width=3,
    marker_end=arrow1.get_funciri()))
sphere.add(gR)

doc.save()

Lizenz

Ich, der Urheberrechtsinhaber dieses Werkes, veröffentliche es hiermit unter der folgenden Lizenz:

Es ist erlaubt, die Datei unter den Bedingungen der GNU-Lizenz für freie Dokumentation, Version 1.2 oder einer späteren Version, veröffentlicht von der Free Software Foundation, zu kopieren, zu verbreiten und/oder zu modifizieren; es gibt keine unveränderlichen Abschnitte, keinen vorderen und keinen hinteren Umschlagtext.

Der vollständige Text der Lizenz ist im Kapitel GNU-Lizenz für freie Dokumentation verfügbar.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue

Diese Datei ist unter der Creative-Commons-Lizenz „Namensnennung 3.0 nicht portiert“ lizenziert.

Dieses Werk darf von dir

verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
neu zusammengestellt werden – abgewandelt und bearbeitet werden

Zu den folgenden Bedingungen:

Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.

Du darfst es unter einer der obigen Lizenzen deiner Wahl verwenden.

Dateiversionen

Klicke auf einen Zeitpunkt, um diese Version zu laden.

	Version vom	Vorschaubild	Maße	Benutzer	Kommentar
aktuell	18:44, 31. Aug. 2014		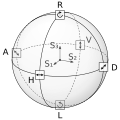600 × 600 (6 KB)	Geek3	Poincare Sphere with Stokes vectors and polarisation arrows

Dateiverwendung

Die folgende Seite verwendet diese Datei:

Poincaré-Kugel

Globale Dateiverwendung

Die nachfolgenden anderen Wikis verwenden diese Datei:

Verwendung auf ar.wikipedia.org
- كرة بوانكاريه

Metadaten

Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.

Kurztitel	poincare-sphere_arrows.svg
Bildtitel	Drawing of a poincare-sphere with polarisations H, V, D, A, R and L, a coordinate system of Stokes-Vectors P1, P2 and P3 and six little images that illustrate the polarisations rights: GNU Free Documentation license, Creative Commons Attribution ShareAlike license
Breite	600
Höhe	600

Datei:Poincare-sphere arrows.svg

Beschreibung

Source Code

Lizenz

Kurzbeschreibungen

In dieser Datei abgebildete Objekte

Motiv

Poincaré sphere ^Englisch

Urheber

Einige Werte ohne einen Wikidata-Eintrag

Urheberrechtsstatus

urheberrechtlich geschützt

Lizenz

GNU-Lizenz für freie Dokumentation Version 1.2 oder später

Creative Commons Namensnennung 3.0 Unported

Datum der Gründung, Erstellung, Entstehung, Erbauung

31. August 2014

Quelle der Datei

durch Hochlader/in erstelltes Original

Dateiversionen

Dateiverwendung

Globale Dateiverwendung

Metadaten

Datei:Poincare-sphere arrows.svg

Beschreibung

Source Code

Lizenz

Kurzbeschreibungen

In dieser Datei abgebildete Objekte

Poincaré sphere Englisch

Einige Werte ohne einen Wikidata-Eintrag

31. August 2014

Dateiversionen

Dateiverwendung

Globale Dateiverwendung

Metadaten

Poincaré sphere ^Englisch