Datei:VFPt dipoles magnetic.svg

Originaldatei (SVG-Datei, Basisgröße: 840 × 840 Pixel, Dateigröße: 103 KB)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Beschreibung
| BeschreibungVFPt dipoles magnetic.svg |
English: Computed drawings of four different types of magnetic dipoles. Upper left: An ideal point-like dipole. The field shape is scale invariant and approximates the field of any magnetized volume with nonzero dipole moment at large distance. |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Geek3 |
| Andere Versionen | VFPt dipoles electric.svg |
| SVG‑Erstellung InfoField | Dieser Plot wurde mit VectorFieldPlot erstellt. |
| Quelltext InfoField | Python code# paste this code at the end of VectorFieldPlot 2.5
R = 0.6
h = 0.6
rsym = 21
doc = FieldplotDocument('VFPt_dipoles_magnetic1', commons=True,
width=360, height=360)
field = Field([ ['dipole', {'x':0, 'y':0, 'px':0., 'py':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return hypot(*xy) > 1e-4 and (fabs(xy[1]) < 1e-3 or fabs(xy[1]) > .3)
nlines = 19
startpoints = Startpath(field, lambda t: 0.25*sc.array([sin(t), cos(t)]),
t0=-pi/2, t1=pi/2).npoints(nlines)
for p0 in startpoints:
line = FieldLine(field, p0, directions='both')
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw dipole symbol
rg_grad = etree.SubElement(doc._get_defs(), 'linearGradient')
rg_grad.set('id', 'grad_rg')
for attr, val in [ ['x1', '0'], ['x2', '0'], ['y1', '0'], ['y2', '1'] ]:
rg_grad.set(attr, val)
for col, of in [ ['#00cc00', '0'], ['#887744', '0.5'], ['#ff0000', '1'] ]:
stop = etree.SubElement(rg_grad, 'stop')
stop.set('stop-color', col)
stop.set('offset', of)
stop.set('stop-opacity', '1')
symb = doc.draw_object('g', {'id':'dipole_symbol',
'transform':'scale({0},{0})'.format(1./doc.unit)})
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#grad_rg)', 'stroke':'none'}, group=symb)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'},
group=symb)
doc.draw_object('path', {'fill':'#000000', 'stroke':'none',
'd':'M 3,-12 V 0 H 12 L 0,15 L -12,0 H -3 V -12 H 3 Z'}, group=symb)
doc.write()
doc = FieldplotDocument('VFPt_dipoles_magnetic2', commons=True,
width=360, height=360)
field = Field([ ['monopole', {'x':0, 'y':h, 'Q':1}],
['monopole', {'x':0, 'y':-h, 'Q':-1}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return fabs(xy[0]) < 1.4
nlines = 18
stp = Startpath(field, lambda t: R*sc.array([.2*sin(t), 1+.2*cos(t)]),
t0=-pi, t1=pi)
startpoints = [stp.startpos(s) for s in sc.arange(nlines)/float(nlines)]
startpoints.append(startpoints[nlines//2].dot([ [1,0],[0,-1] ]))
for p0 in startpoints:
line = FieldLine(field, p0, directions='both', maxr=100)
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw pole symbols
symb_N = doc.draw_object('g', {'id':'north_symbol',
'transform':'translate(0,{0}) scale({1},{1})'.format(h, 1./doc.unit)})
symb_S = doc.draw_object('g', {'id':'south_symbol',
'transform':'translate(0,{0}) scale({1},{1})'.format(-h, 1./doc.unit)})
for i, g in enumerate([symb_N, symb_S]):
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym, 'stroke':'none',
'fill':['#ff0000', '#00cc00'][i]}, group=g)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'}, group=g)
text = etree.SubElement(g, 'text')
for attr, val in [ ['text-anchor', 'middle'], ['x', 0], ['y', 11],
['fill', '#000000'], ['stroke', 'none'], ['font-size', '32px'],
['font-family', 'Bitstream Vera Sans'],
['transform', 'scale(1, -1)'] ]:
text.set(attr, str(val))
text.text = ['N', 'S'][i]
doc.write()
doc = FieldplotDocument('VFPt_dipoles_magnetic3', commons=True,
width=360, height=360)
field = Field([ ['ringcurrent', {'x':0, 'y':0, 'R':R, 'phi':pi/2, 'I':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return hypot(*xy) > R and fabs(fabs(xy[0]) - 1.4) > 0.2
nlines = 13
startpoints = Startpath(field, lambda t: sc.array([R*t, 0.]),
t0=-0.8, t1=0.8).npoints(nlines)
for p0 in startpoints:
line = FieldLine(field, p0, directions='both')
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw current symbols
symb_out = doc.draw_object('g', {'id':'out_symbol',
'transform':'translate({0},0) scale({1},{1})'.format(-R, 1./doc.unit)})
symb_in = doc.draw_object('g', {'id':'in_symbol',
'transform':'translate({0},0) scale({1},{1})'.format(R, 1./doc.unit)})
for i, g in enumerate([symb_out, symb_in]):
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym, 'stroke':'none',
'fill':'#999999'}, group=g)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'}, group=g)
if i == 0: # dot
c_symb = etree.SubElement(g, 'circle')
c_symb.set('cx', '0')
c_symb.set('cy', '0')
c_symb.set('r', '6')
else: # cross
c_symb = etree.SubElement(g, 'path')
c_symb.set('d', 'M {1},{4} L {0},{5} L {2},{3} L {0},{1} \
L {1},{0} {3},{2} L {5},{0} L {4},{1} L {6},{3} L {4},{5} L {5},{4} \
L {3},{6} L {1},{4} Z'.format(12.24, 8, 4.24, 0, -12.24, -8, -4.24))
c_symb.set('style', 'fill:#000000; stroke:none')
doc.write()
doc = FieldplotDocument('VFPt_dipoles_magnetic4', commons=True,
width=360, height=360)
field = Field([ ['coil', {'x':0, 'y':0, 'phi':pi/2, 'R':R, 'Lhalf':h, 'I':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return sc.hypot(xy[0], xy[1]) > R
nlines = 13
for iline in range(nlines):
p0 = sc.array([R * (-1. + 2. * (iline + 0.5) / nlines), 0.])
line = FieldLine(field, p0, directions='both', maxr=100)
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw solenoid
sheet_out = doc.draw_object('g', {
'transform':'translate({0},0)'.format(-R)})
sheet_in = doc.draw_object('g', {
'transform':'translate({0},0)'.format(R)})
for i, g in enumerate([sheet_out, sheet_in]):
doc.draw_object('rect', {'stroke-width':0.03, 'stroke-linejoin':'round',
'x':-0.045, 'y':-h, 'width':0.09, 'height':2*h,
'stroke':'#000000', 'fill':'#bbbbbb'}, group=g)
nsym = 12
for isym in range(nsym):
y = (h - 0.015) * (2 * (isym + 0.5) / nsym - 1)
if i == 0:
doc.draw_object('circle', {'cx':'0', 'cy':y, 'r':0.02,
'fill':'#000000', 'stroke':'none'}, group=g)
else:
doc.draw_object('path', {'d':'M -2,-2 L 2,2 M -2,2 L 2,-2',
'fill':'none', 'stroke':'#000000',
'transform':'translate(0, {0}) scale(0.012)'.format(y),
'stroke-width':'1', 'stroke-linecap':'butt'}, group=g)
doc.write()
|
Lizenz
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
11. Januar 2020
image/svg+xml
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 17:25, 11. Jan. 2020 | 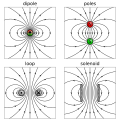 | 840 × 840 (103 KB) | Geek3 | User created page with UploadWizard |
Dateiverwendung
Die folgende Seite verwendet diese Datei:
Globale Dateiverwendung
Die nachfolgenden anderen Wikis verwenden diese Datei:
- Verwendung auf bn.wikipedia.org
- Verwendung auf en.wikipedia.org
- Verwendung auf zh-min-nan.wikipedia.org
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| Kurztitel | VFPt_dipoles_magnetic |
|---|---|
| Bildtitel | VFPt_dipoles_magnetic
created with VectorFieldPlot 2.5 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_dipoles_magnetic.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Breite | 840 |
| Höhe | 840 |