Zyklus der Präzession
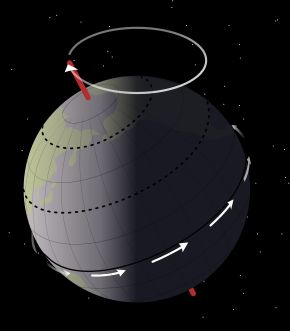
Als Zyklus der Präzession, auch Großes Jahr, Platonisches Jahr oder Weltjahr, wird die Präzessionsperiode der Erdachse von etwa 25.700 bis 25.800 Jahren bezeichnet. In diesem Zeitraum präzediert die Erdachse, die schräg zur Ebene der Ekliptik steht, einmal um die Achse durch den Erdmittelpunkt, die senkrecht auf der Ekliptik steht. Dadurch wandert der Frühlingspunkt einmal durch alle Tierkreiszeichen (Sternbilder). Er zählt zu den sogenannten Milanković-Zyklen.
Ursachen und Zahlenwerte
BearbeitenDie Präzession wird verursacht durch die Gezeitenkräfte einiger Himmelskörper auf die sich drehende Erde. Durch den Äquatorwulst, d. h. der Erdradius am Äquator ist größer als an den Polen, verursachen diese Gezeitenkräfte ein Drehmoment, das versucht, die Rotationsachse der Erde in die Senkrechte zur Ekliptik zu drehen, genaueres unter Präzession der Erdachse.
Beiträge zur Präzessionskonstanten sind:
- die Gezeitenkräfte von Mond und Sonne mit zusammen 50,40" pro Jahr, davon 30" durch den Mond
- die planetarische Präzession von 0,12" pro Jahr
- die geodätische Präzession von 0,02" pro Jahr durch die Allgemeine Relativitätstheorie.
Alle diese Beträge sind nicht konstant. Da ihre Änderungen nur begrenzt berechenbar sind, kann der Zyklus der Präzession bisher nur auf etwa ein Jahrhundert geschätzt werden. Eine genauere Berechnung der genannten Werte gilt in diesem Sinne als spekulativ.[1]
Die Präzessionsdrift der Tierkreiszeichen gegenüber den Sternbildern
BearbeitenDer Zyklus der Präzession ist die Zeit, nach der man genau ein tropisches Jahr mehr zählt als siderische Jahre. Die Länge dieser beiden Jahre unterliegt – für so lange Zeiträume – trotz prinzipiell exakter Definition solchen Ungenauigkeiten, dass eine exaktere Angabe als auf ein Jahrhundert genau nicht sinnvoll erscheint. Darüber hinaus sind die Geschwindigkeit der Präzession und sogar der Öffnungswinkel des Präzessionskegels (die doppelte Schiefe der Ekliptik) über so lange Zeiträume deutlichen Änderungen unterworfen.
Mit der Bewegung des Himmelspols (der Projektion der Erdachse auf die Himmelssphäre) korreliert die Drift des Frühlingspunktes (auch Präzessionsdefekt genannt): Auf einer Sternkarte präzediert der Frühlingspunkt auf einer Linie senkrecht zur Linie vom Himmelspol zum Ekliptikpol, der sich im Zentrum des Präzessionskreises befindet (siehe Abbildung).
Dieser Effekt wurde bereits vor über sechstausend Jahren von den Sumerern bemerkt, als sie in ihrer ältesten und südlichsten Stadt Eridu aufgrund der Präzession zum ersten Mal den Stern Canopus beobachten konnten, wie er direkt über dem Horizont auf dem südlichen Meridian kulminierte. Der Stern wurde auf Sumerisch in der Folge „Stern der Stadt Eridu“ genannt.[3][4]
Anstelle von Frühlingspunkt wird in der Astrologie der seltene Begriff Widderpunkt verwendet, da der Frühlingspunkt den Beginn der zwölf Tierkreiszeichen, jeweils 30°-Abschnitte auf der Ekliptik, bei 0° des Tierkreiszeichens Widder markiert.[5]
Die Präzession ist der Grund für das Auseinanderdriften der Tierkreiszeichen und der Sternbilder, die ihnen den Namen gaben. Der Frühlingspunkt bzw. Widderpunkt befindet sich zurzeit im westlichen Teil des Sternbildes Fische, ist also inzwischen etwa 25° vom Widder entfernt. So lässt sich das Alter dieser Bezeichnung anhand der Präzessionsgeschwindigkeit von 360° in 25.750 Jahren abschätzen: je nachdem, ob der Widderpunkt ursprünglich den Anfang oder die Mitte des Sternbildes Widder markierte, dürfte er seinen Namen vor grob 1700 bis 3000 Jahren bekommen haben. Leider ist die Quellenlage astronomischer Literatur in der vorarabischen Zeit unzureichend. Die Präzession an sich dürfte den babylonischen Astronomen um und vor 300 v. Chr. unbekannt gewesen sein; Gegenteiliges hatte man vorübergehend vor einigen Jahrzehnten vermutet, konnte es aber nicht ausreichend erhärten.[6]
Trotz dieser Vorbehalte ist der Zyklus der Präzession eine Methode der Geschichte der Astronomie und der Astronomischen Chronologie zur Analyse alter himmelskundlicher Aufzeichnungen. Mittels der Frühlingspunktdrift lässt sich etwa eine erstaunlich frühe Wurzel der chinesischen Kalenderrechnung – bis etwa ins 15. Jahrhundert v. Chr. – vermuten[7] oder die Tradition der noch immer im Umlauf befindlichen Bauernkalender ins ausgehende Mittelalter datieren.[8]
Platon und das Platonische Jahr
BearbeitenDie Namensgebung „Platonisches Jahr“ bezieht sich auf den griechischen Philosophen Platon. In seinem Dialog Timaios spricht dieser aber hauptsächlich davon, dass die Planeten im Laufe langer Zeiträume wieder in ihrem gemeinsamen Anfangs- und Frühlingspunkt zusammentreffen und dabei einen Weltzyklus vollenden;[9] die Präzession kommt hierbei nicht vor. Weiterhin wird betont, dass Platon noch gar nichts von der Präzession gewusst haben konnte, da diese erst später durch Hipparchos entdeckt worden sei. Bei dem spätantiken Autor Macrobius findet sich jedoch ein eindeutiger Hinweis auf eine Verknüpfung des Großen Jahres bzw. Weltjahres mit dem Präzessionszyklus der Sterne, so dass dieses Konzept zumindest spätantiken Ursprungs ist. Platon selbst hat an einer anderen Stelle des Timaios auch davon gesprochen, dass die Sterne im Laufe sehr langer Zeiträume bzw. Zyklen von ihren Orten systematisch abweichen, wie er von den „Ägyptern“ erfahren haben will. Dies deutet darauf hin, dass er zumindest ein vages Verständnis des Präzessions-Zyklus besaß und somit auch die Zuweisung „Platonisches Jahr“ gerechtfertigt ist.[10]
Zwölf Platonische Monate
BearbeitenDas Platonische Jahr wird in zwölf Platonische Monate (Weltmonate, Große Monate auch Weltzeitalter) zu je etwa 2150 Jahren unterteilt. Das Sternbild, in dem sich der Frühlingspunkt zurzeit befindet, gibt dem Platonsmonat seinen Namen.
Legt man die im Jahr 1930 definierten Grenzen der Sternbilder zugrunde, verläuft die Ekliptik mittlerweile durch 13 Sternbilder – die zwölf Sternbilder des Tierkreises und den Schlangenträger (Ophiuchus). Da die Sternbilder unterschiedlich große Abschnitte auf der Ekliptik einnehmen, müssen sie zunächst auf 30°-Abschnitte gemittelt werden, um auf gleich lange Weltmonate zu kommen. In dieser Angleichung befindet sich der siderische 0°-Widder-Punkt ziemlich genau gegenüber von Spica, das heißt im Jahr 2010 auf 24° Widder im Tierkreis. Aufgrund der Präzession wird der siderische 0°-Widder-Punkt in ungefähr 6 × 72 Jahren auf der Ekliptik bei 0° Stier angekommen und somit genau 30° vom Frühlingspunkt entfernt sein – auf den sich dann das (angeglichene) Sternbild Wassermann bewegt.
Durch die Präzession wandern die Tagundnachtgleichen und die Sonnenwenden einmal durch alle Sternbilder im Tierkreis. Legt man zwölf Sternbilder mit je 30°, also gleich lange Platonische Monate, sowie eine Periode von 25.800 Jahren zugrunde, dann ergeben sich die Werte für die Weltmonate in folgender Tabelle. Alle anderen Werte in der Tabelle zeigen die Dauer der durch die astronomischen Sternbildgrenzen definierten Zeitphasen (in der Tabelle sind die Weltmonate gerundet auf halbe Jahrhunderte, Hauptstellungen auf Jahrzehnte):
| (in Präzessionsabfolge) | 12 × 30° Sektoren | Eintritt in das Sternbild (13 unterschiedlich breite Sektoren) |
Breite | im Sektor | |||
| Sternbild | Weltmonat | Frühlingspunkt | Sommerpunkt | Herbstpunkt | Winterpunkt | Sektor | Dauer |
| Jungfrau | + 12950 − 12850 |
+ 12170 − 13630 |
− 7180 | − 730 | + 5720 | 44,1° | 3160 Jahre |
|---|---|---|---|---|---|---|---|
| Löwe | − 10700 | − 10470 | − 4020 | + 2430 | + 8880 | 35,7° | 2570 Jahre |
| Krebs | − 8550 | − 7900 | − 1450 | + 5000 | + 11450 | 20,1° | 1440 Jahre |
| Zwillinge | − 6400 | − 6460 | − 10 | + 6440 | + 12890 − 12910 |
27,9° | 2000 Jahre |
| Stier | − 4250 | − 4460 | + 1990 | + 8440 | − 10910 | 36,7° | 2620 Jahre |
| Widder | − 2100 | − 1840 | + 4610 | + 11060 | − 8290 | 24,7° | 1770 Jahre |
| Fische | + 50 | − 70 | + 6380 | + 12830 − 12970 |
− 6520 | 37,2° | 2670 Jahre |
| Wassermann | + 2200 | + 2600 | + 9050 | − 10300 | − 3850 | 24,0° | 1710 Jahre |
| Steinbock | + 4350 | + 4310 | + 10760 | − 8590 | − 2140 | 28,0° | 2010 Jahre |
| Schütze | + 6500 | + 6320 | + 12770 − 13030 |
− 6580 | − 130 | 33,3° | 2380 Jahre |
| Schlangenträger | + 8650 | + 8700 | − 10650 | − 4200 | + 2250 | 18,6° | 1340 Jahre |
| Skorpion | + 10040 | − 9310 | − 2860 | + 3590 | 6,7° | 480 Jahre | |
| Waage | + 10800 | + 10520 | − 8830 | − 2380 | + 4070 | 23,0° | 1650 Jahre |
Die Jahreszahlen sind als Messpunkte auf einer unter Astronomen gebräuchlichen Zeitskala zu verstehen. Der Nullpunkt ist hierbei derselbe wie bei der gebräuchlichen Jahreszählung unseres Kalenders. Da aber auf einer Skala mit Nullpunkt gemessen wird, kann im Vergleich zur bei Historikern verbreiteten Jahreszählung eine Differenz von einem Jahr im Bereich v. u. Z. auftreten. Die zur Bestimmung der Zeitalter verwendeten Sternbilder sind nicht zu verwechseln mit den Tierkreiszeichen, so dass sich bei deren Berücksichtigung eine andere Relation ergeben würde. Wenn also beispielsweise Anfang Januar die Sonne im Tierkreiszeichen Steinbock steht, befindet sie sich räumlich im Sternbild Schütze.[11]
Mutmaßliche Zusammenhänge zwischen Präzessionszyklus und Religionen
BearbeitenDie Entdeckung des Zyklus der Präzession durch den griechischen Astronomen Hipparchos um 128 v. Chr. erschütterte seinerzeit erheblich die gelehrten Kreise, da man doch die großen Himmelskreise des Äquators und der Ekliptik bis dahin als unveränderlich und Sinnbild des Ewigen betrachtet hatte. Dennoch scheint es keinen Beleg dafür zu geben, dass dieser Zyklus in der griechischen Philosophie mit Weltuntergangsspekulationen verknüpft wurde.
Allerdings stellte der Religionswissenschaftler David Ulansey 1989 die Theorie auf, die Entdeckung der Präzession des Frühlingspunktes im 2. Jahrhundert v. Chr. hätte sich unmittelbar auf die Entstehung des Mithraskultes ausgewirkt: Mithras, der von ihm mit dem Sternbild Perseus identifiziert wird, sei gewissermaßen der „Gott der Präzession“.[12]
Die neureligiöse Bewegung Thelema geht ebenfalls von einem Wechsel der Äonen mit dem Wandern des Frühlingspunktes aus.
Langfristige Abweichungen
BearbeitenDer Winkel der Präzessionsachse gegen die Ekliptik (Schiefe der Ekliptik) beträgt derzeit ca. 23,44°, variiert aber aufgrund von Gravitationseinflüssen der anderen Körper im Sonnensystem mit einer Periode von ca. 41.000 Jahren zwischen ca. 22,1° und 24,5°. Diese Änderung des Neigungswinkels (derzeit in Richtung Minimum) sowie weitere langfristige Schwankungen der Bewegung der Erde um die Sonne haben als Milanković-Zyklen Auswirkungen auf die empfangene Strahlungsintensität und beeinflussen das langfristige Klima.
Weblinks
Bearbeiten- Die Präzession auf astronomie.de
Einzelnachweise
Bearbeiten- ↑ Joachim Krautter, Erwin Sedlmayr et al.: Meyers Handbuch Weltall. ISBN 3-411-07757-3, S. 49 ff., besonders S. 51.
- ↑ J. Vondrák, N. Capitaine, P. Wallace: New precession expressions, valid for long time intervals. In: Astronomy & Astrophysics. 534. Jahrgang, 1. Oktober 2011, ISSN 0004-6361, S. A22, doi:10.1051/0004-6361/201117274 (englisch, aanda.org).
- ↑ Markus Bautsch, Friedhelm Pedde: Canopus, der "Stern der Stadt Eridu". In: Wilhelm-Foerster-Sternwarte e.V. / Zeiss-Planetarium am Insulaner (Hrsg.): Dem Himmel nahe. Mitteilungen der Wilhelm-Foerster-Sternwarte e.V. Nr. 17, Mai 2023, ISSN 2940-9330, S. 8–9 (wfs.berlin [PDF; abgerufen am 16. Dezember 2023]).
- ↑ Canopus / Mesopotamien – Wikibooks, Sammlung freier Lehr-, Sach- und Fachbücher. Abgerufen am 16. Dezember 2023.
- ↑ Jürgen Hamel: Begriffe der Astrologie. Verlag Harri Deutsch, Frankfurt am Main 2010, S. 263.
- ↑ Otto Neugebauer: The Alleged Babylonian Discovery of the Precession of the Equinoxes, in: Otto Neugebauer, Astronomy and History. Selected Essays. Springer Verlag, New York/Berlin/Heidelberg 1983, S. 247 ff.
- ↑ Joseph Needham: Wissenschaft und Zivilisation in China. Übers. von Rainer Herbster, Von Colin A. Ronan bearbeitete Ausg., Suhrkamp, Frankfurt am Main 1984, ISBN 3-518-57692-5.
- ↑ Gottfried Briemle: Der Unterschied zwischen Sternzeichen und Sternbildern. In: Oberösterreichischer Volkskalender 2002. Verlag Oberösterr. Bauernbund, Linz, S. 71–78.
- ↑ Timaios 39d
- ↑ Franz Krojer: Etwas zum Ursprung des Platonischen Jahrs. In: Astronomie der Spätantike, die Null und Aryabhata. Differenz-Verlag, München 2009, S. 49–61. (PDF)
- ↑ Massimo Pigliucci: Nonsense on Stilts. How to Tell Science from Bunk. University of Chicago Press, Chicago 2010, S. 63 f.
- ↑ David Ulansey: Die Ursprünge des Mithraskultes. Stuttgart 1998, S. 68–76. Originalausgabe: The Origins of the Mithraic Mysteries: Cosmology and Salvation in the Ancient World. Oxford University Press, New York 1991. Zu einer Kritik von Ulansey Thesen siehe insbesondere Roger Beck: In the Place of the Lion: Mithras in the Tauroctony. In: J. R. Hinnells (Hrsg.): Studies in Mithraism: Papers associated with the Mithraic Panel organized on the occasion of the XVIth Congress of the International Association for the History of Religions. L’Erma di Bretschneider, Rom 1994, S. 29–50.