Császár-Polyeder
Das Császár-Polyeder ist ein nicht-konvexes Polyeder mit einem Loch, bestehend aus 14 Dreiecks-Seiten, 21 Kanten und 7 Ecken. Es hat keine Diagonalen und ist neben dem Tetraeder das einzige bekannte Polyeder mit dieser Eigenschaft (mit der zusätzlichen Voraussetzung, Rand einer Mannigfaltigkeit zu sein).[1] Jedes Eckenpaar ist durch eine Kante verbunden.
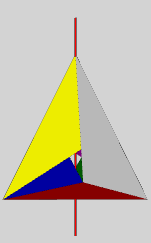
Das Polyeder hat die Topologie eines Torus (Euler-Charakteristik )
Es wurde 1949 von Ákos Császár eingeführt.[2]
Es ist dual zum Szilassi-Polyeder.
