Einheitsdistanz-Graph

Ein Einheitsdistanz-Graph ist ein geometrischer Graph, bei dem jede Kante gleich lang ist. Kanten eines Einheitsdistanz-Graphen dürfen sich überschneiden, d. h. der Graph muss nicht immer planar sein. Ein Einheitsdistanz-Graph ohne Überschneidungen wird Streichholzgraph genannt.

Der Petersen-Graph ist ein Einheitsdistanz-Graph: er kann so gezeichnet werden, dass jede Kante gleich lang ist.

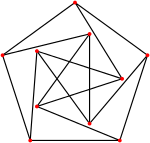
Das Problem von Hadwiger und Nelson beschäftigt sich mit der chromatischen Zahl des Graphen. Jeder Einheitsdistanz-Graph kann mit höchstens sieben Farben eingefärbt werden, bekanntlich existieren aber auch einige Graphen, die mindestens vier Farben benötigen. Ein anderes bekanntes offenes Problem befasst sich mit der Frage, wie hoch das Verhältnis von Kanten- zu Knotenanzahl sein kann.

Beispiele

Hyperwürfel-Graph Q₄ als Einheitsdistanz-Graph.

Folgende Graphen sind Einheitsdistanz-Graphen:

• Jeder zyklische Graph
• Jeder Gittergraph
• Jeder Hyperwürfel-Graph
• Der Petersen-Graph
• Der Heawood-Graph
• Das Wagenrad W₇

Strikter Einheitsdistanz-Graph

Einheitsdistanz-Variante des Möbius–Kantor-Graphen, bei dem einige nicht benachbarte Knoten ebenfalls eine Einheitsdistanz haben.

Einige Definitionen in der Literatur lassen die Möglichkeit zu, dass nicht benachbarte Knotenpaare ebenfalls Einheitsdistanz haben dürfen. Zum Beispiel gibt es eine Variante des Möbius–Kantor-Graphen von dieser Art.

Nach dieser abgeschwächten Definition sind alle verallgemeinerten Petersen-Graphen Einheitsdistanz-Graphen. Um beide Definitionen zu unterscheiden, wird ein Graph, bei dem nur benachbarte Knoten eine Einheitsdistanz haben dürfen, strikter Einheitsdistanz-Graph genannt.

Entfernt man beim Wagenrad W₇ eine Speiche, erhält man einen nicht-strikten Teilgraphen. Es ist nicht möglich, die Knoten und insbesondere die beiden Endpunkte der fehlenden Speiche so anzuordnen, dass man wieder einen strikten Graphen erhält.

Zählung von Einheitsdistanzen

Paul Erdős stellte 1946 das Problem, wie man in einer Menge von n Punkten die Anzahl an Punktpaaren mit Einheitsdistanz bestimmt. Graphentheoretisch formuliert: wie dicht kann ein Einheitsdistanz-Graph sein?

Der Hyperwürfel-Graph besitzt für die Anzahl an Einheitsdistanzen eine untere Schranke proportional zu n·log n. Werden die Punkte in einem Quadratgitter mit vorsichtig gewählten Zwischenräumen angeordnet, gibt es nach Erdős eine verbesserte untere Schranke von

$n^{1+c/\log \log n},$

Erdős bot ein Preisgeld von 500 $, falls jemand eine ähnliche Funktion für die obere Schranke findet. Die beste bekannte obere Schranke liegt bisher proportional zu

$n^{4/3};$

Diese Grenze kann auch als Zählung der Inzidenzen zwischen Punkten und Einheitskreisen betrachtet werden und ist nah mit dem Satz von Szemerédi und Trotter für Inzidenzen zwischen Punkten und Geraden verwandt. Das Problem (Einheitsdistanz-Problem von Erdös) ist nach wie vor offen. Erdös vermutete, dass die Anzahl der Punkte mit Einheitsdistanz in der Größenordnung der unteren Schranke war.

Verallgemeinerung für höhere Dimensionen

Die Definition des Einheitsdistanz-Graphen kann selbstverständlich auch auf höherdimensionale euklidische Räume verallgemeinert werden. Jeder Graph kann als Punktmenge in eine genügend hohe Dimension eingebettet werden. Maehara und Vojtěch Rödl zeigten 1990, dass die notwendige Dimension um einen Graph auf diese Weise einzubetten durch den doppelten Maximalgrad des Graphen beschränkt ist.

Die notwendige Dimension um einen Graphen so einzubetten, dass alle Kanten Einheitsdistanz haben, und die notwendige Dimension um einen Graphen so einzubetten, dass alle Kanten genau den Einheitsdistanz-Paaren entsprechen, können sich stark voneinander unterscheiden: der Johnson-Graph mit 2·n Knoten kann so in die vierte Dimension eingebettet werden, dass all seine Kanten Einheitsdistanz haben, benötigt jedoch n - 2 Dimensionen für eine Einbettung, bei der nur die Kanten Einheitsdistanz-Paare sind.

Siehe auch

• Satz von Beckman und Quarles

Literatur

• F. S. Beckman, D. A. Quarles: On isometries of Euclidean spaces. In: Proceedings of the American Mathematical Society. Band 4, 1953, S. 810–815 (MR0058193). 
• Paul Erdős: On sets of distances of n points. In: American Mathematical Monthly. Band 53 (5). The American Mathematical Monthly, Vol. 53, No. 5, 1946, S. 248–250, doi:10.2307/2305092, JSTOR:2305092. 
• Paul Erdős, Miklós Simonovits: On the chromatic number of geometric graphs. In: Ars Combinatoria. Band 9, 1980, S. 229–246. 
• Eberhard H.-A. Gerbracht: Eleven unit distance embeddings of the Heawood graph. 2009, arxiv:0912.5395. 
• Severino V. Gervacio, Yvette F. Lim, Hiroshi Maehara: Planar unit-distance graphs having planar unit-distance complement. In: Discrete Mathematics. Band 308 (10), 2008, S. 1973–1984, doi:10.1016/j.disc.2007.04.050. 
• Greg Kuperberg: The Erdos kitty: At least $9050 in prizes! 1992 (Posting in der Usenet-Gruppe rec.puzzles and sci.math). 
• Hiroshi Maehara: Distances in a rigid unit-distance graph in the plane. In: Discrete Applied Mathematics. Band 31 (2), 1991, S. 193–200, doi:10.1016/0166-218X(91)90070-D. 
• Hiroshi Maehara: Extending a flexible unit-bar framework to a rigid one. In: Discrete Mathematics. Band 108 (1–3), 1992, S. 167–174, doi:10.1016/0012-365X(92)90671-2 (MR1189840). 
• Hiroshi Maehara, Vojtech Rödl: On the dimension to represent a graph by a unit distance graph. In: Graphs and Combinatorics. Band 6 (4), 1990, S. 365–367, doi:10.1007/BF01787703. 
• Alexander Soifer: The Mathematical Coloring Book. Springer-Verlag, 2008, ISBN 978-0-387-74640-1. 
• Joel Spencer, Endre Szemerédi, William T. Trotter: Unit distances in the Euclidean plane. In: Graph Theory and Combinatorics. Academic Press, 1984, S. 293–308. 
• Apoloniusz Tyszka: Discrete versions of the Beckman-Quarles theorem. In: Aequationes Mathematicae. Band 59 (1–2), 2000, S. 124–133, doi:10.1007/PL00000119 (MR1741475). 
• Arjana Žitnik, Boris Horvat, Tomaž Pisanski: All generalized Petersen graphs are unit-distance graphs. Band 1109, 2010 (online [PDF; 377 kB] IMFM preprints). 

Weblinks

• Suresh Venkatasubramanian: Problem 39: Distances among Point Sets in R² and R³. In: The Open Problems Project. Abgerufen am 16. Oktober 2011. 
• Eric W. Weisstein: Unit-Distance Graph. In: MathWorld (englisch).