Linealgeometrie

Die Linealgeometrie bezeichnet die Einschränkung von Konstruktionsaufgaben der euklidischen Geometrie, bei der der Zirkel nicht verwendet werden darf (und somit auch keine Winkel oder anderen Zeichengeräte). Lediglich das Lineal (ohne Skaleneinteilung) darf verwendet werden. Manchmal wird auch zum Beispiel die Verwendung eines einzelnen Kreises zusätzlich erlaubt, die weitere Konstruktion darf dann aber nur noch mit dem Lineal erfolgen. Die Bezeichnung stammt von Johann Heinrich Lambert (in seinem Buch Freye Perspective, Zürich 1759, 1774). Die Linealgeometrie wurde außer von August Ferdinand Möbius vor allem von Jakob Steiner und Karl Georg Christian von Staudt ausgebaut. Von Steiner und Jean Victor Poncelet stammt der Satz, dass Konstruktionen mit Zirkel und Lineal auch mit Lineal und einem vorgegebenen Kreis ausgeführt werden können.

Linealgeometrie, Halbierung einer Strecke

Beispiele

Tangenten an Kreis

Bild 1: Tangenten an Kreis

Gegeben sei ein Punkt $A$ und ein Kreis (Mittelpunkt nicht bekannt). Gesucht sind die beiden Tangenten von $A$ an den Kreis (siehe Bild 1). In der Linealgeometrie erhält man die Lösung folgendermaßen: Man zieht von $A$ aus zwei Sekanten durch den Kreis und erhält die Punkte $P_{1}$ bis $P_{4}.$ Es folgen die Verbindungen der Punkte $P_{1}$ mit $P_{4}$ und $P_{2}$ mit $P_{3}$ sowie die Halbgeraden ab $P_{3}$ durch $P_{1}$ und ab $P_{4}$ durch $P_{2};$ dabei ergeben sich die Schnittpunkte $X$ bzw. $P.$ Zieht man jetzt eine Linie von $P$ durch $X$ bis zum Kreis, erhält man die beiden Tangentenpunkte $T_{1}$ und $T_{2}.$

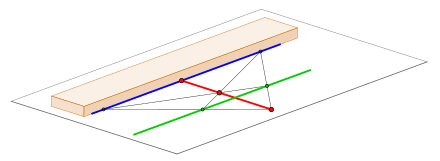
Parallele zu einer Geraden

Es ist nicht möglich, mit dem Lineal allein eine Parallele zu einer gegebenen Geraden zu zeichnen. Ist jedoch auf der Geraden eine Strecke und deren Halbierungspunkt – wie im Bild 2 dargestellt – gegeben, kann man eine Parallele zur Geraden konstruieren.

Es sei ${\overline {FG}}$ eine Strecke auf einer Geraden, $D$ der Halbierungspunkt von ${\overline {FG}}$ sowie $H$ ein Punkt, durch den die gesuchte Parallele zu ${\overline {FG}}$ verlaufen soll.

Man beginnt mit einer Halbgeraden ab $G$ durch $H$ und einem darauf beliebig festgelegten Punkt $A.$ Es folgen die Verbindungen der Punkte $F$ mit $H,$ $F$ mit $A$ sowie $D$ mit $A$; dabei ergibt sich der Schnittpunkt $C.$ Nun zieht man eine gerade Linie ab $G$ durch $C$ bis sie die Strecke ${\overline {FA}}$ in $J$ schneidet. Die abschließende Gerade durch $H$ und $J$ ist die gesuchte Parallele.

Bild 2: Parallele durch $H$ zur gegebenen Strecke ${\overline {FG}},$ nach Steiner

Halbierungspunkt einer Strecke

Es ist nicht möglich, mit dem Lineal allein eine Strecke zu halbieren. Ist jedoch zu einer Strecke eine Parallele – wie im Bild 3 dargestellt – vorgegeben, kann man den Halbierungspunkt der Strecke konstruieren.

Gegeben sei eine Strecke ${\overline {FG}}$ und eine Parallele zu ${\overline {FG}}.$ Gesucht ist der Halbierungspunkt der Strecke ${\overline {FG}}$.

Man beginnt damit, einen beliebig festgelegten Punkt $A$ mit den Punkten $G$ und $F$ zu verbinden; dabei entstehen die Schnittpunkte $H$ bzw. $J.$ Es folgen die Verbindungen der Punkte $F$ mit $H$ sowie $G$ mit $J$; dabei ergibt sich der Schnittpunkt $C.$ Abschließend zieht man eine gerade Linie ab $A$ durch $C$ bis zur Strecke ${\overline {FG}},$ und erhält damit den gesuchten Halbierungspunkt $D$ der Strecke ${\overline {FG}}.$

Bild 3: Halbierungspunkt $D$ der Strecke ${\overline {FG}},$ nach Steiner

Siehe auch

• Satz von Poncelet-Steiner
• Konstruktion des 4. harmonischen Punktes

Quelle

• Linealgeometrie. In: Meyers Großes Konversations-Lexikon, Band 12. Leipzig 1908, S. 572.