In der Trigonometrie stellt der Tangenssatz (auch Tangentensatz und Regel von Napier) eine Beziehung zwischen den drei Seiten eines ebenen Dreiecks und dem Tangens der halben Summe bzw. der halben Differenz zweier Winkel des Dreiecks her.
Formulierung
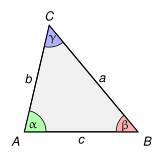
BearbeitenFür die drei Seiten a, b und c eines Dreiecks sowie für die diesen Seiten jeweils gegenüber liegenden Winkel α, β und γ gilt:
Wegen
kann man diese Formel auch schreiben als
Analoge Formeln für und erhält man durch zyklische Vertauschung:
Wegen bleiben diese Formeln gültig, wenn sowohl die Seiten als auch die zugehörigen Winkel vertauscht werden, also etwa:
Beweis mit Sinussatz und Identitäten der Winkelfunktionen
BearbeitenNach dem Sinussatz gilt und damit folgt:
nach Einsetzen der Identitäten
sowie
- ,
die sich aus den Additionstheoremen ableiten lassen, ergibt sich per Division die gewünschte Formel.
Beweis mit Mollweideschen Formeln
BearbeitenMit Winkelsumme im Dreieck und Übergang zum Komplementärwinkel:
- (1)
Aus den Mollweideschen Formeln folgt mit (1):
- q. e. d.
Siehe auch
BearbeitenLiteratur
Bearbeiten- Max Koecher, Aloys Krieg: Ebene Geometrie. Springer 2007, S. 129 (Auszug (Google))
- Johannes Tropfke: Geschichte der Elementarmathematik. Band 5. I: Ebene Trigonometrie. II: Sphärik und sphärische Trigonometrie. Walter de Gruyter, 1923, ISBN 3-11-144776-6, S. 79–82, doi:10.1515/9783111447766.70, Auszug (Google)
Weblinks
Bearbeiten- Eric W. Weisstein: Law of Tangents. In: MathWorld (englisch).