Poisson-Approximation

Die Poisson-Approximation ist in der Wahrscheinlichkeitsrechnung eine Möglichkeit, die Binomialverteilung und die verallgemeinerte Binomialverteilung für große Stichproben und kleine Wahrscheinlichkeiten durch die Poisson-Verteilung anzunähern. Durch den Grenzübergang nach unendlich erhält man dann die Konvergenz in Verteilung der beiden Binomialverteilungen gegen die Poisson-Verteilung.

Vergleich der Poisson-Verteilung (schwarze Linien) und der Binomialverteilung mit $n=10$ (rote Kreise), $n=20$ (blaue Kreise),$n=1000$ (grüne Kreise). Alle Verteilungen haben einen Erwartungswert von 5. Die horizontale Achse zeigt die Anzahl der eingetretenen Ereignisse $k$. Je größer $n$ wird, umso besser ist die Approximation der Binomialverteilung durch die Poisson-Verteilung.

Formulierung

Ist $(S_{n})$ eine Folge binomialverteilter Zufallsvariablen mit Parametern $n\in \mathbb {N}$ und $p_{n}$, sodass für die Erwartungswerte $E(S_{n})=n\cdot p_{n}\to \lambda >0$ für $n\to \infty$ gilt, dann folgt

$P(S_{n}=k)=B_{n,p_{n}}(\{k\})\to \,{\frac {\lambda ^{k}}{k!}}\mathrm {e} ^{-\lambda }=P_{\lambda }(\{k\})\quad$

für $n\to \infty$.

Beweis-Skizze

Der Wert einer Poisson-verteilten Zufallsvariable an der Stelle $k$ ist der Grenzwert $n\to \infty$ einer Binomialverteilung mit $p={\tfrac {\lambda }{n}}$ an der Stelle $k$:

${\begin{aligned}\lim _{n\to \infty }P(S_{n}=k)&=\lim _{n\to \infty }{\binom {n}{k}}p^{k}(1-p)^{n-k}\\&=\lim _{n\to \infty }{\frac {n!}{k!\,(n-k)!}}\left({\frac {\lambda }{n}}\right)^{k}\left(1-{\frac {\lambda }{n}}\right)^{n-k}\\&=\lim _{n\to \infty }\left({\frac {\lambda ^{k}}{k!}}\right)\left({\frac {n(n-1)(n-2)\cdots (n-k+1)}{n^{k}}}\right)\left(1-{\frac {\lambda }{n}}\right)^{n}\left(1-{\frac {\lambda }{n}}\right)^{-k}\\&={\frac {\lambda ^{k}}{k!}}\cdot \lim _{n\to \infty }\underbrace {\left({\frac {n}{n}}\cdot {\frac {n-1}{n}}\cdot {\frac {n-2}{n}}\cdots {\frac {n-k+1}{n}}\right)} _{\to 1}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{n}} _{\to e^{-\lambda }}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{-k}} _{\to 1}\\&={\frac {\lambda ^{k}\mathrm {e} ^{-\lambda }}{k!}}.\end{aligned}}$

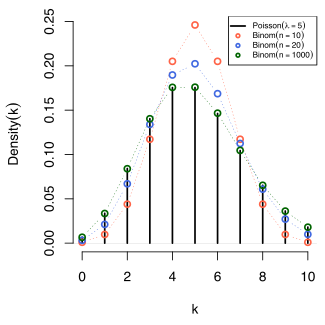
Bei großen Stichproben und kleinem $p$ lässt sich folglich die Binomialverteilung gut durch die Poisson-Verteilung approximieren.

Die Darstellung als Grenzwert der Binomialverteilung erlaubt eine alternative Berechnung von Erwartungswert und Varianz der Poisson-Verteilung. Seien $X_{1},\dotsc ,X_{n}\,n$ unabhängige bernoulliverteilte Zufallsvariablen mit $\,p=\lambda /n$ und sei $S_{n}:=X_{1}+\dotsb +X_{n}$. Für $n\to \infty$ gilt $S_{n}\sim P_{\lambda }$ und

${\begin{aligned}\operatorname {E} (S_{n})&=\operatorname {E} (X_{1})+\dotsb +\operatorname {E} (X_{n})=\underbrace {{\frac {\lambda }{n}}+\dotsb +{\frac {\lambda }{n}}} _{n\,\mathrm {mal} }=\lambda \to \lambda \\\operatorname {Var} (S_{n})&=\operatorname {Var} (X_{1})+\dotsb +\operatorname {Var} (X_{n})\\&=\underbrace {{\frac {\lambda }{n}}\left(1-{\frac {\lambda }{n}}\right)+\dotsb +{\frac {\lambda }{n}}\left(1-{\frac {\lambda }{n}}\right)} _{n\,\mathrm {mal} }=\lambda \left(1-{\frac {\lambda }{n}}\right)\to \lambda .\end{aligned}}$

Güte der Approximation

Für die Fehlerabschätzung gilt

$\sum _{k\geq 0}\left|B_{n,p}(\{k\})-P_{n\cdot p}(\{k\})\right|\leq 2np^{2}$.

Die Approximation einer Summe von Bernoulli-verteilten Zufallsvariablen (bzw. einer binomialverteilten Zufallsvariable) ist also insbesondere für kleine $p$ gut. Als Faustregel gilt, dass die Approximation gut ist, wenn $n\geq 50$ und $p\leq 0{,}05$ gilt. Ist $p\approx 0{,}5$, so ist die Normal-Approximation besser geeignet.

Le Cams Verallgemeinerung

Allgemeiner lässt sich Folgendes zeigen: Seien $X_{1},\dotsc ,X_{n}$ stochastisch unabhängige Zufallsvariablen mit $P(X_{i}=1)=p_{i}=1-P(X_{i}=0)$ (jede Zufallsvariable ist also Bernoulli-verteilt), dann ist

$S:=\sum _{i=1}^{n}X_{i}$

verallgemeinert binomialverteilt. Definiere

$\lambda :=\sum _{i=1}^{n}p_{i}$,

dann gilt

$\sum _{k=0}^{\infty }\left|P(S=k)-\exp(-\lambda ){\frac {\lambda ^{k}}{k!}}\right|\leq 2\sum _{i=1}^{n}p_{i}^{2}$.

Im Englischen ist dieses Resultat als „Ungleichung von Le Cam“ (Le Cam’s Inequality) bekannt.

Gilt $p_{i}=p_{j}$ für alle $1\leq i,j\leq n$, so ist $S$ binomialverteilt und das obige Ergebnis folgt sofort.

Beispiel

Ein Individuum einer Spezies zeugt $n=1000$ Nachkommen, die alle stochastisch unabhängig voneinander mit einer Wahrscheinlichkeit von $p_{i}=0{,}001$ das geschlechtsreife Alter erreichen. Interessiert ist man nun an der Wahrscheinlichkeit, dass zwei oder mehr Nachkommen das geschlechtsreife Alter erreichen.

Exakte Lösung

Sei $X_{i}=1$ die Zufallsvariable „Der $i$-te Nachkomme erreicht das geschlechtsreife Alter“. Es gilt $P(X_{i}=1)=p_{i}$ und $P(X_{i}=0)=1-p_{i}$ für alle $i$. Dann ist die Anzahl der überlebenden Nachkommen $S:=\sum _{i=1}^{n}X_{i}$ aufgrund der stochastischen Unabhängigkeit $B_{n,p}$-verteilt. Zur Modellierung definiert man den Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ mit der Ergebnismenge $\Omega :=\{0,\dotsc ,n\}$, der Anzahl der überlebenden geschlechtsreifen Nachkommen. Die σ-Algebra ist dann kanonisch die Potenzmenge der Ergebnismenge: $\Sigma :={\mathcal {P}}(\Omega )$ und als Wahrscheinlichkeitsverteilung die Binomialverteilung: $P(\{k\}):=B_{n,p}(\{k\})$. Gesucht ist $P(S\geq 2)=1-P(S=1)-P(S=0)=1-B_{1000;\,0{,}001}(\{0\})-B_{1000;\,0{,}001}(\{1\})\approx 0{,}2642$. Es erreichen also mit einer Wahrscheinlichkeit von ca. 26 % mindestens zwei Individuen das geschlechtsreife Alter.

Approximierte Lösung

Da $n$ ausreichend groß und $p$ ausreichend klein ist, lässt sich die Binomialverteilung genügend genau mittels der Poisson-Verteilung annähern. Diesmal ist der Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ definiert mittels des Ergebnisraums $\Omega :=\mathbb {N}$, der $\sigma$-Algebra $\Sigma :={\mathcal {P}}(\mathbb {N} )$ und der Poisson-Verteilung als Wahrscheinlichkeitsverteilung $P(\{k\}):=P_{\lambda }(\{k\})={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }$ mit dem Parameter $\lambda =n\cdot p=1$. Man beachte hier, dass die beiden modellierten Wahrscheinlichkeitsräume unterschiedlich sind, da die Poisson-Verteilung auf einem endlichen Ergebnisraum keine Wahrscheinlichkeitsverteilung definiert. Die Wahrscheinlichkeit, dass mindestens zwei Individuen das geschlechtsreife Alter erreichen, ist also $P(S\geq 2)\approx 1-P_{\lambda }(\{1\})-P_{\lambda }(\{0\})=1-{\frac {\lambda ^{1}}{1!}}e^{-1}-{\frac {\lambda ^{0}}{0!}}e^{-1}\approx 0{,}2642$.

Bis auf vier Nachkommastellen stimmt also die exakte Lösung mit der Poisson-Approximation überein.

Weblinks

• A.V. Prokhorov: Poisson theorem. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org). 

• Eric W. Weisstein: Poisson theorem. In: MathWorld (englisch).

Literatur

• Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin Heidelberg 2013, ISBN 978-3-642-36017-6, doi:10.1007/978-3-642-36018-3. 
• Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. Für Studium, Berufspraxis und Lehramt. 8. Auflage. Vieweg, Wiesbaden 2005, ISBN 3-8348-0063-5, doi:10.1007/978-3-663-09885-0. 
• Hans-Otto Georgii: Stochastik. Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7, doi:10.1515/9783110215274.