Porroprisma
Das Porroprisma, benannt nach seinem Erfinder Ignazio Porro, der es 1854[1] patentieren ließ, ist das klassische Umkehrprisma in einem traditionellen Fernglas mit Keplerschen Fernrohren. Ein Porroprisma besteht in der Regel aus zwei einfachen rechtwinkligen Reflexionsprismen – sogenannten Halbwürfelprismen –, die vom Lichtstrahl nacheinander passiert werden. Da die zwei Halbwürfelprismen in ihrer Lage zueinander um 90° gedreht sind, erzeugt die vierfache Reflexion des Lichtstrahles beim Passieren eines Porroprismas insgesamt eine 180°-Drehung des Bildes. Die von einem Keplerfernrohr hervorgerufene 180°-Drehung des Originalbildes wird durch das Porroprisma somit aufgehoben.
Der Strahlengang wird in einem Halbwürfelprisma zweimal, also geradzahlig, reflektiert, so dass das Bild seitenrichtig bleibt. Er wird dabei um 180° umgelenkt, was im ersten Halbwürfelprisma zum Aufrichten des kopfstehenden Bildes ausgenutzt wird, es wird kopfüber gewendet. Die nicht gewollte 180°-Ablenkung – man müsste mit dem Fernrohr nach hinten beobachten – wird mit Hilfe des zweiten Prismas kompensiert. Damit wird das Bild um eine vertikale Achse gewendet, und das Fernrohr bleibt geradsichtig. Ein dem Aufrichten des kopfstehenden Bildes analoger Vorgang entfällt, weil der Beobachter die zweite Wende des Strahlengangs mitmacht. Der ersten Wende folgt er nicht, denn er stellt sich nicht selbst auf den Kopf. Die zu erfüllende Bedingung lautet in physikalisch-optischer Formulierung wie folgt: Das Bild wird vollständig umgekehrt, wenn die Reflexionen in zwei verschiedenen Hauptschnitten eines Prismensystems stattfinden.[2]
Daneben gibt es noch das Porroprisma 2. Art[3], das ebenfalls den Strahlengang viermal 90° umlenkt. Ein doppelt reflektierendes Halbwürfelprisma ist zwischen zwei kleineren nur je einmal reflektierenden Halbwürfelprismen platziert. Die Hauptschnitte der äußeren Prismen sind zum mittleren Prisma rechtwinklig angeordnet. Sein Vorteil ist, dass vertikal kein Versatz des Strahlengangs erfolgt. Eine weitere Variante mit gleicher Funktion ist das aus zwei Teilprismen zusammengesetzte Porro-Abbe-Prisma.[4]
Die zweiteilige Ausführung des Porroprismas 2. Art ist zum Perger-Prisma weiterentwickelt worden, welches durch geänderte Winkel der Reflexionsflächen und der Kittfläche die Eigenschaften verbindet, einen nur kleinen Versatz des Strahlengangs zu erfordern und dabei zusätzlich zu ermöglichen, einen Messstrahl oder eine beleuchtete Anzeige einzuspiegeln. Perger-Prismen werden z. B. in kompakten Ferngläsern mit integriertem Entfernungsmesser benutzt.
-
Zweimal reflektierter Strahlengang in einem Halbwürfelprisma
-
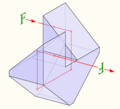
Strahlengang in einem Halbwürfelprismenpaar (Porroprisma)
-
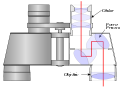
Schematischer Querschnitt durch ein Porroprismen-Fernglas
-
Querschnitt durch ein Porroprismen-Fernglas
-
Strahlengang in einem Porroprisma 2. Art
-
Strahlengang im Perger-Prisma (Kittfläche blau)
Nebeneffekte
Bearbeiten- Durch die Faltung des Strahlengangs verkürzt sich die Baulänge des Fernrohrs um bis zu 60 Prozent (z. B. bei einem Fernglas 7×50 von etwa 40 cm (Brennweite des Objektivs) auf rund 15 cm).
- Der gegenseitige Abstand der Teilferngläser vergrößert sich, sodass das räumliche Sehen merklich verbessert, die Naheinstellung allerdings erschwert wird.
- Durch den größeren Abstand der Teilferngläser kann deren Durchmesser und damit die Lichtstärke größer sein.
Als Bauelement in Ferngläsern steht das Porroprisma heute in Konkurrenz zum geradsichtigen Dachkant-Pentaprisma. Letzteres ist geometrisch aufwändiger, erlaubt aber eine weniger breite Bauweise der Ferngläser (zu Ungunsten des räumlichen Sehens, siehe 2.). Der für kompakte Außenabmessungen eines Fernglases erwünschte, kleinere Versatz des Strahlengangs lässt sich auch mit dem 2012 patentierten Perger-Prisma erzielen, welches dabei die prinzipiellen Nachteile des Dachkantprismas vermeidet.
Siehe auch
Bearbeiten- Porro-Spiegelsucher
- Dachkantprisma, ebenfalls bei Ferngläsern verbreitet
Weblinks
BearbeitenEinzelnachweise
Bearbeiten- ↑ Patent GB195402377: Certain applications of total or partial reflection of light on transparent surfaces either alone or combined with the reflection. Veröffentlicht am 9. November 1854 (Auf Espace derzeit nicht einsehbar).
- ↑ Fritz Hodam: Technische Optik. VEB Verlag Technik Berlin, 1967, S. 254.
- ↑ Heinz Haferkorn: Optik - Physikalisch-technische Grundlagen und Anwendungen. Barth, Leipzig 1994, ISBN 3-335-00363-2, S. 485.
- ↑ M. Bass (Hrsg.): Handbook of Optics. Volume I - Geometrical and Physical Optics, Polarized Light, Components and Instruments. 3. Auflage. McGraw-Hill Professional Publishing, 2009, ISBN 978-0-07-162925-6, S. 19.6.