Inhaltsverzeichnis
1 Semester 1
1.1 Zeit, Raum, Bewegung 1.2 Masse, Stoffmenge 1.3 Impuls, Kraft, Felder 1.4 Arbeit, Leistung, Energie 1.5 Wellen 1.6 Ladung, Strom, Spannung 1.7 Größe, Einheit, Dimension 1.8 Stromkreis 1.9 elektrisches Feld 1.10 Kondensatoren 1.11 verteilte elektrische Ströme 1.12 Berechnung elektrischer Felder 1.13 Eigenschaften elektrischer Felder
2 Semester 2
Beschleunigung, Geschwindigkeit, Position:
a
→
=
v
→
˙
=
r
→
¨
{\displaystyle {\vec {a}}={\dot {\vec {v}}}={\ddot {\vec {r}}}}
Richtung
e
→
{\displaystyle {\vec {e}}}
R
3
{\displaystyle \mathbb {R} ^{3}}
e
→
=
e
→
x
cos
α
x
+
e
→
y
cos
α
y
+
e
→
z
cos
α
z
{\displaystyle {\vec {e}}={\vec {e}}_{x}\,\cos \alpha _{x}+{\vec {e}}_{y}\,\cos \alpha _{y}+{\vec {e}}_{z}\,\cos \alpha _{z}}
ρ
=
m
V
{\displaystyle \rho ={\frac {m}{V}}}
m
=
n
⋅
M
{\displaystyle m=n\cdot M}
Impuls
p
→
=
m
⋅
v
→
{\displaystyle {\vec {p}}=m\cdot {\vec {v}}}
Kraft
F
→
=
m
⋅
a
→
{\displaystyle {\vec {F}}=m\cdot {\vec {a}}}
Inertialsystem )Gravitationsgesetz
F
→
=
G
m
1
⋅
m
2
r
2
e
→
r
{\displaystyle {\vec {F}}=G\,{\frac {m_{1}\cdot m_{2}}{r^{2}}}\,{\vec {e}}_{r}}
Gravitationsfeldstärke
g
→
=
F
→
m
2
=
G
m
1
r
2
e
→
r
{\displaystyle {\vec {g}}={\frac {\vec {F}}{m_{2}}}=G\,{\frac {m_{1}}{r^{2}}}\,{\vec {e}}_{r}}
wird durch Bezug auf m 2 unabhängig von Beeinflussung durch Messung (Masse des Messgeräts)
Coulomb-Gesetz
F
→
=
1
4
π
ε
0
Q
1
⋅
Q
2
r
2
e
→
r
{\displaystyle {\vec {F}}={\frac {1}{4\,\pi \,\varepsilon _{0}}}\,{\frac {Q_{1}\cdot Q_{2}}{r^{2}}}\,{\vec {e}}_{r}}
siehe auch: Elementarladung (e) elektrische Feldstärke
E
→
=
F
→
Q
=
1
4
π
ε
0
Q
1
r
2
e
→
r
{\displaystyle {\vec {E}}={\frac {\vec {F}}{Q}}={\frac {1}{4\,\pi \varepsilon _{0}}}\,{\frac {Q_{1}}{r^{2}}}\,{\vec {e}}_{r}}
(Kraft je Ladungseinheit) Arbeit
1
J
=
1
N
m
=
1
k
g
m
2
s
2
{\displaystyle 1\,\mathrm {J} =1\,\mathrm {Nm} =1\,{\frac {\mathrm {kg} \,\mathrm {m} ^{2}}{\mathrm {s} ^{2}}}}
W
=
F
→
⋅
s
→
{\displaystyle W={\vec {F}}\cdot {\vec {s}}}
Arbeit wird (zB. bei Hindernis) nur in „Verschieberichtung“ geleistet:
W
=
F
→
⋅
s
⋅
cos
α
{\displaystyle W={\vec {F}}\cdot s\cdot \cos \alpha }
Zerlegung in Komponenten:
F
→
=
F
→
1
+
F
→
2
{\displaystyle {\vec {F}}={\vec {F}}_{1}+{\vec {F}}_{2}}
F
→
1
=
F
⋅
cos
α
{\displaystyle {\vec {F}}_{1}=F\cdot \cos \alpha }
F
→
2
=
F
⋅
sin
α
{\displaystyle {\vec {F}}_{2}=F\cdot \sin \alpha }
konservatives Kraftfeld
Arbeit wird verrichtet und verlusstfrei zurückgewonnen.
W
=
F
i
s
i
=
0
{\displaystyle W=F_{i}\,s_{i}=0}
Leistung
1
W
=
1
J
s
=
1
N
m
s
=
1
k
g
m
2
s
3
{\displaystyle 1\,\mathrm {W} =1\,{\frac {\mathrm {J} }{\mathrm {s} }}=1\,{\frac {\mathrm {Nm} }{\mathrm {s} }}=1\,{\frac {\mathrm {kg} \,\mathrm {m} ^{2}}{\mathrm {s} ^{3}}}}
P
=
W
˙
=
F
→
⋅
v
→
{\displaystyle P={\dot {W}}={\vec {F}}\cdot {\vec {v}}}
Hauptsätze der Thermodynamik Energieerhaltungssatz Wärme kann nicht vollständig in Arbeit umgewandelt werden
→ Abwärme ; absolute thermodynamische Temperatur
T Periodendauer
Amax - Amin
Schwankung
k Kreiswellenzahl
c Ausbreitungsgeschwindigkeit
f
=
1
T
{\displaystyle f={\frac {1}{T}}}
ω
=
2
π
f
=
φ
˙
{\displaystyle \omega =2\,\pi \,f={\dot {\varphi }}}
Sinusschwingung (harmonische Schwingung)
w
=
w
^
sin
(
k
t
−
ω
t
)
{\displaystyle w={\hat {w}}\,\sin \left(k\,t-\omega \,t\right)}
mit
λ
=
2
π
k
{\displaystyle \lambda =2\,\pi \,k}
c
=
ω
k
=
λ
f
=
λ
T
{\displaystyle c={\frac {\omega }{k}}=\lambda \,f={\frac {\lambda }{T}}}
Wellen in Festkörpern Dispersion
unterschiedliche Ausbreitungsgeschwindigkeit (Lichtbrechung) Ladungsdichte elektrischer Strom
I
=
Q
˙
{\displaystyle I={\dot {Q}}}
magnetische Kraft zweier Leiter
1
C
=
1
A
s
{\displaystyle 1\,\mathrm {C} =1\,\mathrm {As} }
F
→
l
→
=
μ
0
I
1
I
2
2
π
r
→
{\displaystyle {\frac {\vec {F}}{\vec {l}}}=\mu _{0}\,{\frac {I_{1}\,I_{2}}{2\,\pi \,{\vec {r}}}}}
magnetische Feldkonstante
1
V
s
A
m
=
1
k
g
m
A
2
s
2
{\displaystyle 1\,{\frac {\mathrm {V} \,\mathrm {s} }{\mathrm {A} \,\mathrm {m} }}=1\,{\frac {\mathrm {kg} \,\mathrm {m} }{\mathrm {A} ^{2}\,\mathrm {s} ^{2}}}}
μ
0
=
4
π
10
−
7
V
s
A
m
{\displaystyle \mu _{0}=4\,\pi \,10^{-7}\,{\frac {\mathrm {V} \,\mathrm {s} }{\mathrm {A} \,\mathrm {m} }}}
Elektrische Spannung
1
V
=
1
m
2
k
g
s
3
A
{\displaystyle 1\,\mathrm {V} =1\,{\frac {\mathrm {m} ^{2}\,\mathrm {kg} }{\mathrm {s} ^{3}\,\mathrm {A} }}}
U
=
W
Q
=
E
i
s
i
{\displaystyle U={\frac {W}{Q}}=E_{i}\,s_{i}}
U
=
R
I
=
P
I
{\displaystyle U=R\,I={\frac {P}{I}}}
U
=
Δ
φ
{\displaystyle U=\Delta \varphi }
wichtige Einheiten außerhalb SI
atomare Masseneinheit
1
u
≈
1,661
10
−
27
k
g
{\displaystyle 1\,\mathrm {u} \approx 1{,}661\,10^{-27}\,\mathrm {kg} }
Elektronenvolt
1
e
V
≈
1
,
602
10
−
19
J
{\displaystyle 1\,\mathrm {eV} \approx 1,602\,10^{-19}\,\mathrm {J} }
wichtige physikalische Konstanten
Lichtgeschwindigkeit
c
0
≈
300
⋅
10
6
m
s
{\displaystyle c_{0}\approx 300\cdot 10^{6}\,{\frac {\mathrm {m} }{\mathrm {s} }}}
Elementarladung
e
≈
1,602
⋅
10
−
16
A
s
{\displaystyle e\approx 1{,}602\cdot 10^{-16}\,\mathrm {A} \,\mathrm {s} }
Ruhemasse des Elektrons
m
e
≈
9
,
11
⋅
10
−
31
k
g
{\displaystyle m_{e}\approx 9{,}11\cdot 10^{-31}\,\mathrm {kg} }
Ruhemasse des Protons
m
p
≈
1,673
⋅
10
−
27
k
g
{\displaystyle m_{p}\approx 1{,}673\cdot 10^{-27}\,\mathrm {kg} }
magnetische Feldkonstante
μ
0
=
4
π
⋅
10
−
7
V
s
A
m
{\displaystyle \mu _{0}=4\,\pi \cdot 10^{-7}\,{\frac {\mathrm {V} \,\mathrm {s} }{\mathrm {A} \,\mathrm {m} }}}
elektrische Feldkonstante
ε
0
=
1
μ
0
c
0
2
≈
8,854
p
F
m
{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}\,c_{0}^{2}}}\approx 8{,}854\,{\frac {\mathrm {pF} }{\mathrm {m} }}}
Avogadro-Konstante
N
A
≈
6,022
⋅
10
23
1
m
o
l
{\displaystyle N_{A}\approx 6{,}022\cdot 10^{23}\,{\frac {1}{\mathrm {mol} }}}
Boltzmann-Konstante
k
≈
1,381
⋅
10
−
23
J
K
{\displaystyle k\approx 1{,}381\cdot 10^{-23}\,{\frac {\mathrm {J} }{\mathrm {K} }}}
Planck-Konstante
h
≈
6,626
⋅
10
−
34
J
s
{\displaystyle h\approx 6{,}626\cdot 10^{-34}\,\mathrm {J} \,\mathrm {s} }
magnetisches Moment des Elektrons
μ
e
≈
9,285
⋅
10
−
24
A
m
2
{\displaystyle \mu _{e}\approx 9{,}285\cdot 10^{-24}\,\mathrm {A} \,\mathrm {m} ^{2}}
Maxwell-Beziehung
ε
0
μ
0
c
0
2
=
1
{\displaystyle \varepsilon _{0}\,\mu _{0}\,c_{0}^{2}=1}
siehe auch:
Kirchhoffsche Regeln Kirchhoffsche Regel (Knotenregel)
∑
I
=
0
{\displaystyle \sum I=0}
Kirchhoffsche Regel (Maschenregel)
∑
U
=
0
{\displaystyle \sum U=0}
elektrischer Widerstand
U
=
R
I
{\displaystyle U=R\,I}
G
=
R
−
1
{\displaystyle G=R^{-1}}
Leitwert )
P
=
R
I
2
=
U
2
R
{\displaystyle P=R\,I^{2}={\frac {U^{2}}{R}}}
spezifischer Widerstand (Resistivität ) ρ
R
=
ρ
⋅
l
A
{\displaystyle R=\rho \cdot {\frac {l}{A}}}
elektrische Leitfähigkeit (Konduktivität ) γ
γ
=
1
ρ
{\displaystyle \gamma ={\frac {1}{\rho }}}
Diode
U
D
=
U
D
′
+
I
D
⋅
R
B
{\displaystyle U_{D}=U'_{D}+I_{D}\cdot R_{B}}
R
B
=
0
,
1
…
10
Ω
{\displaystyle R_{B}=0{,}1\dots 10\,\mathrm {\Omega } }
U
B
R
=
0
,
65
…
0
,
7
V
{\displaystyle U_{BR}=0{,}65\dots 0{,}7\,\mathrm {V} }
siehe auch: Stern-Dreieck-Schaltung , Stern-Polygon-Transformation
Φ
{\displaystyle \Phi }
magnetischer Fluss
W
b
=
T
m
2
=
V
s
{\displaystyle \mathrm {Wb} =\mathrm {T\,m^{2}} =\mathrm {V\,s} }
Q
{\displaystyle Q}
elektrische Ladung
A
s
=
C
{\displaystyle \mathrm {A\,s} =\mathrm {C} }
E
{\displaystyle E}
elektrische Feldstärke
V
m
{\displaystyle \mathrm {\frac {\mathrm {V} }{\mathrm {m} }} }
U
{\displaystyle U}
elektrische Spannung
V
{\displaystyle \mathrm {V} }
Ψ
{\displaystyle \Psi }
elektrischer Fluss
A
s
{\displaystyle \mathrm {A\,s} }
λ
{\displaystyle \lambda }
Linienladungsdichte
A
s
m
{\displaystyle \mathrm {\frac {A\,s}{m}} }
σ
{\displaystyle \sigma }
Flächenladungsdichte
A
s
m
2
{\displaystyle \mathrm {\frac {A\,s}{m^{2}}} }
ρ
{\displaystyle \rho }
Raumladungsdichte
A
s
m
3
{\displaystyle \mathrm {\frac {A\,s}{m^{3}}} }
D
{\displaystyle D}
elektrische Flussdichte
A
s
m
2
{\displaystyle \mathrm {\frac {A\,s}{m^{2}}} }
Ω
{\displaystyle \Omega }
Raumwinkel
s
r
=
1
{\displaystyle \mathrm {sr} =1}
C
{\displaystyle C}
elektrische Kapazität
F
=
C
V
=
A
s
V
{\displaystyle \mathrm {F} ={\frac {\mathrm {C} }{\mathrm {V} }}={\frac {\mathrm {A} \,\mathrm {s} }{\mathrm {V} }}}
ε
{\displaystyle \varepsilon }
Permittivität
F
m
=
C
V
=
A
2
s
4
k
g
m
2
{\displaystyle {\frac {\mathrm {F} }{\mathrm {m} }}={\frac {\mathrm {C} }{\mathrm {V} }}={\frac {\mathrm {A} ^{2}\,\mathrm {s} ^{4}}{\mathrm {kg} \,\mathrm {m} ^{2}}}}
ε
r
{\displaystyle \varepsilon _{r}}
Permittivitätszahl
1
{\displaystyle 1}
elektrische Feldstärke
E
=
−
d
Φ
d
l
{\displaystyle \mathbf {E} =-{\frac {\mathrm {d} \Phi }{\mathrm {d} \mathbf {l} }}}
U
=
E
s
{\displaystyle \mathbf {U} =\mathbf {E} \,\mathbf {s} }
elektrischer Fluss , Influenz
Ψ
(
∂
V
)
=
Q
(
V
)
{\displaystyle \mathbf {\Psi } \left(\partial V\right)=\mathbf {Q} \left(V\right)}
Ψ
=
D
A
{\displaystyle \mathbf {\Psi } =\mathbf {D} \,\mathbf {A} }
Ladungsdichte
Q
=
ρ
V
=
σ
A
=
λ
l
{\displaystyle \mathbf {Q} =\mathbf {\rho } \,\mathbf {V} =\mathbf {\sigma } \,\mathbf {A} =\mathbf {\lambda } \,\mathbf {l} }
elektrische Flussdichte
D
=
Q
A
=
σ
e
r
=
ε
0
E
{\displaystyle \mathbf {D} ={\frac {Q}{\mathbf {A} }}=\mathrm {\sigma } \,\mathbf {e} _{r}=\varepsilon _{0}\,\mathbf {E} }
magnetischer Fluss
Φ
=
B
A
=
Q
ε
0
{\displaystyle \Phi =\mathbf {B} \,\mathbf {A} ={\frac {Q}{\varepsilon _{0}}}}
Punktladung
D
=
d
Ψ
d
A
=
Q
4
π
r
2
e
→
r
{\displaystyle \mathbf {D} ={\frac {\mathrm {d} \mathbf {\Psi } }{\mathrm {d} \mathbf {A} }}={\frac {Q}{4\,\pi \,r^{2}}}\,{\vec {e}}_{r}}
E
=
D
ε
0
=
Q
4
π
r
2
ε
0
e
→
r
{\displaystyle \mathbf {E} ={\frac {\mathbf {D} }{\varepsilon _{0}}}={\frac {Q}{4\,\pi \,r^{2}\,\varepsilon _{0}}}\,{\vec {e}}_{r}}
elektrische Kapazität
C
=
Q
U
{\displaystyle C={\frac {Q}{U}}}
Plattenkondensator
C
=
ε
0
A
l
{\displaystyle C=\varepsilon _{0}\,{\frac {A}{l}}}
Kugelkondensator
E
→
=
−
Δ
φ
Δ
l
→
=
1
ε
0
4
π
⋅
Q
r
→
(
r
→
+
Δ
r
→
)
{\displaystyle {\vec {E}}=-{\frac {\Delta \varphi }{\Delta {\vec {l}}}}={\frac {1}{\varepsilon _{0}\,4\,\pi }}\cdot {\frac {Q}{{\vec {r}}\,\left({\vec {r}}+\Delta {\vec {r}}\right)}}}
U
=
Q
ε
0
4
π
(
1
r
1
−
1
r
2
)
{\displaystyle U={\frac {Q}{\varepsilon _{0}\,4\,\pi }}\,\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right)}
C
=
ε
0
4
π
r
1
r
2
r
2
−
r
1
{\displaystyle C=\varepsilon _{0}\,{\frac {4\,\pi \,r_{1}\,r_{2}}{r_{2}-r_{1}}}}
im leeren Raum (
r
2
≫
r
1
{\displaystyle r_{2}\gg r_{1}}
C
=
ε
0
4
π
r
1
{\displaystyle C=\varepsilon _{0}\,4\,\pi \,r_{1}}
E
=
Q
ε
0
4
π
r
1
2
U
=
Q
ε
0
4
π
r
1
}
E
=
U
r
1
{\displaystyle \left.{\begin{matrix}E={\frac {Q}{\varepsilon _{0}\,4\,\pi \,r_{1}^{2}}}\\U={\frac {Q}{\varepsilon _{0}\,4\,\pi \,r_{1}}}\end{matrix}}\right\}E={\frac {U}{r_{1}}}}
Dielektrika
D
=
ε
E
{\displaystyle \mathbf {D} =\mathbf {\varepsilon } \,\mathbf {E} }
ε
=
ε
0
ε
r
{\displaystyle \mathbf {\varepsilon } =\varepsilon _{0}\,\mathbf {\varepsilon } _{r}}
siehe auch: Maxwellsche Gleichungen , elektrisches Feld , Van-de-Graaff-Generator
Q
=
C
U
{\displaystyle Q=C\,U}
I
=
Q
˙
{\displaystyle I={\dot {Q}}}
⇒
C
=
I
U
˙
{\displaystyle \Rightarrow C=I\,{\dot {U}}}
R-C-Reihenschaltung
U
=
U
C
+
U
R
{\displaystyle U=U_{C}+U_{R}}
I
=
C
U
˙
{\displaystyle I=C\,{\dot {U}}}
U
R
=
R
I
{\displaystyle U_{R}=R\,I}
I
=
U
n
a
c
h
−
U
v
o
n
R
e
−
t
τ
τ
=
R
C
{\displaystyle I={\frac {U_{nach}-U_{von}}{R}}\,e^{-{\frac {t}{\tau }}}\quad \tau =R\,C}
U
C
=
U
n
a
c
h
−
(
U
n
a
c
h
−
U
v
o
n
)
e
−
t
τ
{\displaystyle U_{C}=U_{nach}-\left(U_{nach}-U_{von}\right)\,e^{-{\frac {t}{\tau }}}}
Q
C
=
C
U
C
{\displaystyle Q_{C}=C\,U_{C}}
Umladung nach 5τ praktisch abgeschlossen. elektrische Stromdichte
J
→
=
I
A
→
{\displaystyle {\vec {J}}={\frac {I}{\vec {A}}}}
Flächenstromdichte
K
=
I
s
{\displaystyle K={\frac {I}{s}}}
Linienstrom
I
=
∑
I
l
{\displaystyle I=\sum I_{l}}
lokales Ohmsches Gesetz
U
l
=
ρ
I
A
⇒
E
→
=
ρ
J
→
⇔
J
→
=
γ
E
→
{\displaystyle {\frac {U}{l}}=\rho \,{\frac {I}{A}}\Rightarrow {\vec {E}}=\rho \,{\vec {J}}\Leftrightarrow {\vec {J}}=\gamma \,{\vec {E}}}
Leistung
P
=
U
I
=
R
I
2
=
G
U
2
{\displaystyle P=U\,I=R\,I^{2}=G\,U^{2}}
Joule-Verlusst
p
=
P
V
=
ϱ
J
2
=
γ
E
2
{\displaystyle p={\frac {P}{V}}=\varrho \,J^{2}=\gamma \,E^{2}}
V
=
A
l
{\displaystyle V=A\,l}
Ferromagnetismus wird von Magnet angezogen. (Eisen )
Paramagnetismus wird nicht (kaum) von Magnet beeinflusst. (Aluminium )
Diamagnetismus wird von Magnet abgestoßen. (Wismut ) Stromduchflossener Leiter erzeugt Magnetfeld
B
=
μ
0
I
2
π
r
→
{\displaystyle B={\frac {\mu _{0}\,I}{2\,\pi \,{\vec {r}}}}}
Stromdurchlossenes Element im Magnetfeld erfährt Kraft
F
=
I
l
→
×
B
→
{\displaystyle F=I\,{\vec {l}}\times {\vec {B}}}
Lorentz-Kraft
E
→
=
E
→
+
v
→
×
B
→
;
F
→
=
Q
E
→
{\displaystyle {\vec {E}}={\vec {E}}+{\vec {v}}\times {\vec {B}};\ {\vec {F}}=Q\,{\vec {E}}}
F
→
=
Q
(
E
→
+
v
→
×
B
→
)
{\displaystyle {\vec {F}}=Q\,\left({\vec {E}}+{\vec {v}}\times {\vec {B}}\right)}
Magnetische Spannung um Leiter Flussquant (Fluxoid )
Φ
0
=
h
2
e
≈
2
,
07
⋅
10
−
15
W
b
{\displaystyle \Phi _{0}={\frac {h}{2\,e}}\approx 2{,}07\cdot 10^{-15}\,\mathrm {Wb} }
magnetischer Hüllenfluss
Φ
(
∂
V
)
=
0
{\displaystyle \Phi \left(\partial V\right)=0}
magnetischen Monopole )Verkettungsfluss (Flussverkettung )
Φ
v
=
Ψ
=
n
Φ
{\displaystyle \Phi _{v}=\Psi =n\,\Phi }
n Wicklungen werden von magn. Fluss Φ durchflossen)magnetischer Fluss , magnetische Flussdichte
Φ
(
A
)
=
∫
A
B
d
A
{\displaystyle \Phi \left(A\right)=\int _{A}B\ \mathrm {d} A}
magnetisches Vektorpotenzial
Φ
(
A
)
=
∫
A
d
s
{\displaystyle \Phi \left(A\right)=\int \mathbf {A} \ \mathrm {d} s}
A ist Vektorfeld magnetischer Potenziale; bildet magnetische Potenzialflächen; s ist Kurvenabschitt)magnetische Spannung um Leiter
Θ
(
A
)
=
α
2
π
I
{\displaystyle \Theta \left(A\right)={\frac {\alpha }{2\,\pi }}\,I}
H
=
I
×
r
2
π
r
2
{\displaystyle \mathbf {H} =\mathbf {I} \times {\frac {\mathbf {r} }{2\,\pi \,\mathbf {r} ^{2}}}}
B
=
I
×
μ
r
2
π
r
2
⇒
B
=
μ
H
{\displaystyle \mathbf {B} =\mathbf {I} \times {\frac {\mu \,\mathbf {r} }{2\,\pi \,\mathbf {r} ^{2}}}\Rightarrow \mathbf {B} =\mu \,\mathbf {H} }
μ
=
μ
r
⋅
μ
0
{\displaystyle \mu =\mu _{r}\cdot \mu _{0}}
μ
0
=
4
π
10
−
7
V
s
A
m
=
4
π
10
−
7
H
m
{\displaystyle \mu _{0}=4\,\pi \,10^{-7}\,\mathrm {\frac {V\,s}{A\,m}} =4\,\pi \,10^{-7}\,\mathrm {\frac {H}{m}} }
1
H
=
1
W
b
A
=
1
V
s
A
{\displaystyle 1\,\mathrm {H} =1\,\mathrm {\frac {Wb}{A}} =1\,\mathrm {\frac {V\,s}{A}} }
siehe auch: Joseph Henry Verkettungsfluss eine Induktivität mit mehreren gleichartigen Windungen
Φ
=
N
A
B
→
=
N
A
n
μ
0
I
l
=
L
I
{\displaystyle \Phi =N\,A\,{\vec {B}}=N\,A\,{\frac {n\;\mu _{0}\,I}{l}}=L\,I}
L
=
μ
0
A
N
2
l
{\displaystyle L={\frac {\mu _{0}\,A\,N^{2}}{l}}}
magnetische Kopplung zwei Induktivitäten mit gegenseitiger Beeinflussung für
I
2
=
0
{\displaystyle \,I_{2}=0}
B
=
μ
0
H
=
μ
0
N
1
I
1
1
l
1
{\displaystyle B=\mu _{0}\,H=\mu _{0}\,N_{1}\,I_{1}\,{\frac {1}{l_{1}}}}
Φ
=
N
2
A
2
B
=
μ
0
N
1
N
2
A
2
I
1
l
{\displaystyle \Phi =N_{2}\,A_{2}\,B=\mu _{0}\,N_{1}\,N_{2}\,A_{2}\,I{\frac {1}{l}}}
L
1
,
2
=
μ
0
N
1
N
2
A
2
l
{\displaystyle L_{1,2}=\mu _{0}\,N_{1}\,N_{2}\,{\frac {A_{2}}{l}}}
dünne Hysterese
H
C
>
0
,
5
k
A
m
{\displaystyle H_{C}>0{,}5\,\mathrm {\frac {kA}{m}} }
breite Hysterese
H
C
<
0
,
5
k
A
m
{\displaystyle H_{C}<0{,}5\,\mathrm {\frac {kA}{m}} }
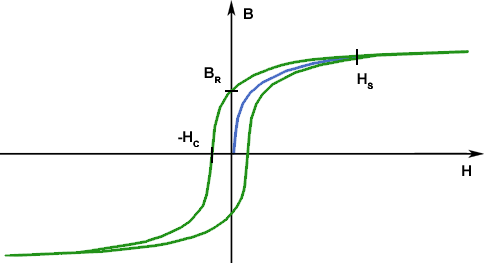
Hysterese Sättigungsmagnetisierung
Die Steigungsrate im Kurvenverlauf stellt die magnetische Leitfähigkeit eines magnetischen Werkstoffes dar. Das Abflachen der Kurve im rechten oberen und linken unteren Bereich stellt den Beginn der für diesen Werkstoff typischen Sättigungsmagnetisierung dar.
Die Permeabilität µ ist Steigung der Hysteresiskurve. Es gilt:
μ
→
μ
(
H
)
{\displaystyle \mu \to \mu \left(H\right)}
Biot-Savart-Gesetz Überlagerung der B-Felder einzelner Ladungen Q in einem Punkt P
B
(
P
)
=
μ
0
4
π
∫
i
Q
i
v
i
×
r
i
r
i
3
d
i
{\displaystyle \mathbf {B} \left(\mathbf {P} \right)={\frac {\mu _{0}}{4\,\pi }}\,\int _{i}{Q_{i}\,\mathbf {v} _{i}\times {\frac {\mathbf {r} _{i}}{\mathbf {r} _{i}^{3}}}}\mathrm {d} i}
Q
v
=
d
d
t
(
Q
s
)
=
I
s
{\displaystyle Q\,\mathbf {v} ={\frac {\mathrm {d} }{\mathrm {d} t}}\left(Q\,s\right)=\mathbf {I} \,\mathbf {s} }
elektrische Größe
magnetische Größe
I
=
U
R
{\displaystyle I={\frac {U}{R}}}
Φ
=
Θ
R
m
{\displaystyle \Phi ={\frac {\Theta }{R_{m}}}}
R
=
l
γ
A
=
1
G
{\displaystyle R={\frac {l}{\gamma \,A}}={\frac {1}{G}}}
R
m
=
l
μ
A
=
1
G
m
{\displaystyle R_{m}={\frac {l}{\mu \,A}}={\frac {1}{G_{m}}}}
∑
I
=
0
{\displaystyle \sum I=0}
∑
Φ
=
0
{\displaystyle \sum \Phi =0}
∑
U
=
0
{\displaystyle \sum U=0}
∑
Θ
=
0
{\displaystyle \sum \Theta =0}
Satz des magnetischen Hüllenflusses
Φ
(
∂
V
)
=
B
n
+
A
+
B
n
−
A
=
0
{\displaystyle \Phi (\partial V)=B_{n}^{+}\,A+B_{n}^{-}\,A=0}
→
[
[
B
n
]
]
=
0
{\displaystyle \rightarrow [\![B_{n}]\!]=0}
→
[
[
A
→
t
]
]
=
0
→
{\displaystyle \rightarrow [\![{\vec {A}}_{t}]\!]={\vec {0}}}
Lokaler Satz des magnetischen Hüllenflusses
∇
B
→
=
0
{\displaystyle \nabla {\vec {B}}=0}
Durchflutungssatz
V
(
∂
A
)
=
I
(
A
)
{\displaystyle V\left(\partial A\right)=I\left(A\right)}
Grundvorstellung Elektromagnetische Induktion
∇
×
E
+
B
˙
=
0
{\displaystyle \nabla \times \mathbf {E} +{\dot {B}}=0}
U
+
Φ
˙
=
0
{\displaystyle U+{\dot {\Phi }}=0}
I
=
U
R
=
−
Φ
˙
R
{\displaystyle I={\frac {U}{R}}={\frac {-{\dot {\Phi }}}{R}}}
U
=
R
I
+
Φ
v
˙
{\displaystyle U=R\,I+{\dot {\Phi _{v}}}}
Wirbelstrom -EindringtiefeWechselströme fließen nur bis zur Eindringtiefe (Skineffekt )
δ
=
2
ω
γ
μ
{\displaystyle \delta ={\sqrt {\frac {2}{\omega \,\gamma \,\mu }}}}
γ
elektrische Leitfähigkeit
μ
Permeabilität
Induktion in bewegten Leitern
E
v
=
E
0
+
v
→
×
B
{\displaystyle \mathbf {E} _{v}=\mathbf {E} _{0}+{\vec {v}}\times \mathbf {B} }
J
=
γ
E
v
{\displaystyle \mathbf {J} =\gamma \,\mathbf {E} _{v}}
Φ
v
=
L
I
{\displaystyle \Phi _{v}=L\,I}
U
=
L
I
˙
{\displaystyle U=L\,{\dot {I}}}
induktiver Lade- und Entladevorgang
τ
=
L
R
{\displaystyle \tau ={\frac {L}{R}}}
U
L
(
t
)
=
(
U
2
−
U
1
)
e
−
t
τ
{\displaystyle U_{L}\left(t\right)=\left(U_{2}-U_{1}\right)\,e^{-{\frac {t}{\tau }}}}
I
(
t
)
=
U
2
−
U
L
(
t
)
R
{\displaystyle I\left(t\right)={\frac {U_{2}-U_{L}\left(t\right)}{R}}}
Trafogrundgleichung
(
U
1
U
2
)
=
(
L
11
L
12
L
21
L
22
)
(
I
˙
1
I
˙
2
)
{\displaystyle {\begin{pmatrix}U_{1}\\U_{2}\end{pmatrix}}={\begin{pmatrix}L_{11}&L_{12}\\L_{21}&L_{22}\end{pmatrix}}\,{\begin{pmatrix}{\dot {I}}_{1}\\{\dot {I}}_{2}\end{pmatrix}}}
Kopplungsgrad
k
12
=
L
12
L
11
L
22
{\displaystyle k_{12}={\frac {L_{12}}{\sqrt {L_{11}\,L_{22}}}}}
M
=
k
L
1
L
2
{\displaystyle M=k\,{\sqrt {L_{1}\,L_{2}}}}
(
U
1
U
2
)
=
(
L
1
M
L
2
M
)
(
I
˙
1
I
˙
2
)
{\displaystyle {\begin{pmatrix}U_{1}\\U_{2}\end{pmatrix}}={\begin{pmatrix}L_{1}&M\\L_{2}&M\end{pmatrix}}\,{\begin{pmatrix}{\dot {I}}_{1}\\{\dot {I}}_{2}\end{pmatrix}}}
Reihenschaltung
L
=
∑
k
L
k
{\displaystyle L=\sum _{k}L_{k}}
L
=
L
1
+
L
2
+
2
M
{\displaystyle L=L_{1}+L_{2}+2\,M}
Mitkopplung )
L
=
L
1
+
L
2
−
2
M
{\displaystyle L=L_{1}+L_{2}-2\,M}
Gegenkopplung )
L
=
∑
k
,
l
L
k
l
{\displaystyle L=\sum _{k,l}L_{kl}}
Parallelschaltung
L
=
L
1
‖
L
2
‖
…
‖
L
k
{\displaystyle L=L_{1}\|L_{2}\|\dots \|L_{k}}
1
L
=
∑
k
1
L
k
{\displaystyle {\frac {1}{L}}=\sum _{k}{\frac {1}{L_{k}}}}
L
=
L
1
L
2
−
M
2
L
1
+
L
2
−
2
M
{\displaystyle L={\frac {L_{1}\,L_{2}-M^{2}}{L_{1}+L_{2}-2\,M}}}
L
=
L
1
L
2
−
M
2
L
1
+
L
2
+
2
M
{\displaystyle L={\frac {L_{1}\,L_{2}-M^{2}}{L_{1}+L_{2}+2\,M}}}








































































































































































![{\displaystyle \rightarrow [\![B_{n}]\!]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb70affbe19d702a6b3f981eee54b1049319e6b3)
![{\displaystyle \rightarrow [\![{\vec {A}}_{t}]\!]={\vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b71def504a05ac43751bba42054232d98e7b26a)

























