Benutzer:Pyrometer/Baustelle/Biegemoment

Dieser Artikel ist im Entstehen und noch nicht Bestandteil der freien Enzyklopädie Wikipedia.

Solltest du über eine Suchmaschine darauf gestoßen sein, bedenke, dass der Text noch unvollständig sein und Fehler oder ungeprüfte Aussagen enthalten kann. Wenn du Fragen zum Thema hast, nimm Kontakt mit dem Autor Pyrometer auf.

Überarbeitung, gestützt auf "Biegemoment" Stand 29. April 2013 um 12:48.
Urbeberrechte evtl. verbliebener Fragmente aus jenem Stand bitte der Versionsgeschichte jenes Standes entnehmen.
Dieses Version ist als Referenz und Diskussionsgrundlage vorgesehen, nicht zum Überschreiben des bestehenden Artikels.

Muster-Anmerkung fett Muster-Anmerkung Muster-Anmerkung

---

Eingespannter Balken mit Endlast (umbeschriften: P->F, L->l)

Balken mit Mittenlast
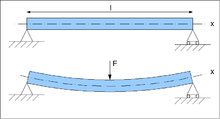
(beschriften: x-Achse)

Als Biegemoment wird ein Drehmoment bezeichnet, das einen Balken, einen Träger oder eine Welle auf Biegung belastet.

Als Biegemoment wird ein Drehmoment bezeichnet, das einen schlanken Körper (dünn relativ zur Länge, wie bei Balken, Träger oder Welle) auf Biegung belastet. Es entsteht durch Kräfte, die an verschiedenen Stellen des Körpers quer auf ihn einwirken.

Ganz alt, aber richtig richtig: Es ist diejenige Schnittreaktion, die zu bestimmen und mit welcher der Biegefall statisch zu berechnen ist.

Verschlimmbesserung ;-): Es ist diejenige Schnittreaktion, die zu bestimmen (ist) und mit ihrder die Verbiegung des Bauteils und die in ihm auftretende Biegespannung zu ermitteln ist.

Dringend 29. Apr: Es entsteht typischerweise durch eine Kraft (Last), die außerhalb der Auflager quer auf den Körper wirkt und ist das Produkt aus Kraft und Hebelarmlänge mit maximalem Wert an der Stelle, wo die Kraft angreift.

Mit nur einer Kraft kommen wir nicht zu einer Erklärung. Und für den eingespannten Balken ist das Maximum auch ganz woanders. Wir kommen am Ende nicht drum herum, explizit (oder implizit) mit Schnitten zu erklären.

---

Mal so ganz am Phänomen (und zunächst ohne Erklärung der Ermittlung): Für das Beispiel des eingespannten Balkens mit Last an freien Ende ist das Biegemoment an der Einspannung maximal und beträgt dort $M=-F\cdot l$. Am freien Ende tritt kein Biegemoment auf.

Für das Beispiel eines Balkens mit Mittenlast ist das Biegemoment an den Enden gleich null und am Mittelpunkt maximal. Es beträgt in der Mitte $M=-F/4$ .

Zusammenhang zwischen äußeren Kräften und dem Momentenverlauf im Balkens aus "Schnitt"

Und nun die Erklärung (Dies meidet den "Schnitt", erklärt dasselbe auf andere Weise.): Für die Ermittlung des Momentes an einer beliebigen Stelle x des Balkens werden diejenigen Drehmomente bezüglich dieses Punktes x addiert, die von Kräften auf einer Seite der Stelle x verursacht werden. (Siehe auch Hauptartikel Schnittreaktion)

Somit ergibt sich der Momentenverlauf für den eingespannten Balken als

$M(x)=-(l-x)\cdot F$

und für den Balken mit Mittenlast als

$M(x)={\begin{cases}-{\frac {F\cdot x}{2}}&{\mbox{für }}0\leq x\leq {\tfrac {l}{2}}\\-{\frac {F\cdot (l-x)}{2}}&{\mbox{für }}{\tfrac {l}{2}}=x\leq l\end{cases}}$

Biegelinie

Das Biegemoment verursacht im Balken innere Spannungen, die wiederum eine Biegung/Krümmung bewirken. Die Stärke der Biegung hängt neben dem Moment $M$ auch von dem E-Modul $E$ des Materials und von der Form der Querschnittsfläche (charakterisiert durch das Flächenmoment $I$) ab. Für den Biegeradius $R$ gilt:

$M(x)=E\cdot I\cdot {\frac {1}{R(x)}}$    

Die Form beziehungsweise die Biegelinie $w(x)$ eines elastisch verbogenen schlanken Bauteiles (Balken) mit konstantem Querschnitt, das einem Biegemoment $M_{y}(x)$ unterworfen ist, kann mit folgender Näherungs-Formel beschrieben werden:

$w''(x)=-{M_{y}(x) \over EI_{y}}$ .     ($w''$ ist die Krümmung der Biegelinie, die in der $xz$ -Ebene (Bildebene) liegt.)

$M(x)=E\cdot I\cdot {\frac {1}{R(x)}}$    

Der Elastizitätsmodul $E$ ist eine Materialeigenschaft, $I_{y}$ ist das axiale Flächenträgheitsmoment (eine rein geometrische Größe) des Balken-Querschnitts, von dem sein Verhalten bei Biegung um die $y$ -Achse abhängt.

Die Krümmung $w''$ ist proportional zum Biegemoment $M_{y}$ . Im Beispiel sind beide in Balkenmitte ($x=l/2$) am größten.

$w''(x=l/2)=-{F\cdot l \over 4\cdot EI_{y}}$ .

Biegespannung

Die durch das Biegemoment verursachte Biegespannung in einem Querschnitt eines Balkens kann wie folgt ermittelt werden:

$\sigma _{B}(z)={\frac {M_{y}(x)}{I_{y}}}z$ .     (zusätzlich variabel in $z$-Koordinate, die im Beispiel vertikal verläuft)

Die Biegespannung $\sigma _{B}$ ist gleich wie die Krümmung des schlanken Bauteils proportional zum Biegemoment $M_{y}$ . Im Beispiel ist sie folglich auch in Balkenmitte ($x=l/2$) am größten.

$\sigma _{B}(z)={\frac {M_{y}(x=l/2)}{I_{y}}}z$ .

Die Höhe der Biegespannung spielt eine Rolle, wenn zu untersuchen ist, ob der Balken die Beanspruchung aushält, sich nicht bleibend verformt oder gar bricht. Sie ist im Balkenquerschnitt proportional zur Entfernung $z$ von der neutralen Faser (in der Regel durch den Schwerpunkt des Querschnitts gehend). Beim maximalen $z_{r}$, das heißt in der oberen Randfaser (Bogeninnenseite) entsteht die größte Druck-Spannung, in der untersten Randfaser (Bogenaußenseite) die größte Zug-Spannung.

Weil bei konstantem Balkenquerschnitt das Flächenträgheitsmoment konstant ist, lässt sich sein Quotient mit dem Abstand der Randfaser $z_{r}$ zum konstanten Widerstandsmoment

$W_{y}=I_{y}/z_{r}$     ( Index $y$ kennzeichnet, dass das Widerstandsmoment für Biegung um $y$-Achse gilt)

zusammen fassen. Für die in der Randfaser auftretende Biegespannung gilt damit die Formel:

$\sigma _{B}(z=z_{r})={\frac {M_{y}(x)}{W_{y}}}$ .

Für das Beispiel entsteht mit den Werten   $x=l/2$   und   $M_{y}=F\cdot l/4$ )
folgende Grenz-Gleichung gegen Biege-Versagen:

$\sigma _{B}(x=l/2)(z=z_{r})={\frac {F\cdot l}{4\cdot W_{y}}}$ .

Siehe auch

• Balkentheorie
• Torsionsmoment
• Moment (Technische Mechanik)
• Statische Berechnung

Weblinks

• Grundlagen - Moment - Skript mit dem Grundwissen der Statik