Bethe-Salpeter-Gleichung

Die Bethe-Salpeter-Gleichung (nach Hans Bethe und Edwin Salpeter 1951) beschreibt Bindungszustände eines quantenfeldtheoretischen Zwei-Körper-Systems.

Eine graphische Darstellung der Bethe-Salpeter-Gleichung

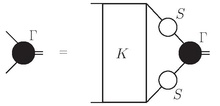
Da die Bethe-Salpeter-Gleichung in vielen Bereichen der Theoretischen Physik ihre Anwendung findet, gibt es auch verschiedene Schreibweisen. Eine Form, wie sie in der Teilchenphysik häufig verwendet wird, ist

$\Gamma (P,p)=\int \!{\frac {d^{4}k}{(2\pi )^{4}}}\;K(P,p,k)\,S{\Bigl (}k-{\frac {P}{2}}{\Bigr )}\,\Gamma (P,k)\,S{\Bigl (}k+{\frac {P}{2}}{\Bigr )}$

wobei Γ die Lösung der Bethe-Salpeter-Gleichung, die Bethe-Salpeter-Amplitude, darstellt, K den Wechselwirkungskern und S jeweils die Propagatoren der Teilchen, die den Bindungszustand bilden (im Folgenden als Konstituenten bezeichnet).

In einer Quantentheorie sind Bindungszustände stabil, das heißt, sie existieren unendlich lange und so können ihre Konstituenten unendlich oft miteinander wechselwirken. Die Bethe-Salpeter-Gleichung beschreibt diese Zustände, indem sie jede mögliche Wechselwirkung, die zwischen den beiden Konstituenten passieren kann, unendlich oft iteriert. Ihre Lösung, die Bethe-Salpeter-Amplitude beschreibt den Bindungszustand, z. B. im Orts- oder im Impulsraum.

Mögliche Anwendungen der Bethe-Salpeter-Gleichung sind das Wasserstoffatom, Positronium, Excitonen und Mesonen.

Herleitung

Eine Herleitung der Bethe-Salpeter-Gleichung basiert auf der Tatsache, dass Bindungszustände Pole in den Greenschen Funktionen der Theorie sind.

Dazu beginnt man mit der Dyson-Gleichung für die 4-Punktfunktionen

$G=S_{1}\,S_{2}+S_{1}\,S_{2}\,K_{12}\,G$

wobei $G$ die 4-Punkt-Green-Funktion $\langle \Omega |{\mathcal {T}}\left\{\phi _{1}\,\phi _{2}\,\phi _{3}\,\phi _{4}\right\}|\Omega \rangle$, $S$ sind die Propagatoren und $K$ der Wechselwirkungskern, der alle Zweiteilchen-irreduziblen Wechselwirkungen enthält.

Mit Hilfe der so genannten Bethe-Salpeter-Wellenfunktionen $\Psi =\langle \Omega |{\mathcal {T}}\left\{\phi _{1}\,\phi _{2}\right\}|\psi \rangle$, die man als Übergangsamplitude der zwei Konstituenten in den Bindungszustand ansehen kann, kann man, in der Nähe des Bindungszustandpoles, die Greensche Funktion ansetzen als

$G={\frac {\Psi \;{\bar {\Psi }}}{P^{2}-M^{2}}}$.

wobei $P$ den Gesamtimpuls des Systems darstellt und $M$ die Masse des gebundenen Zustandes. Für $P^{2}=M^{2}$ hat dieser Ansatz einen Pol was genau der Massenschalenbedingung für relativistische Impulse entspricht.

geht man mit diesem Ansatz in die Dyson-Gleichung oben erhält man

${\frac {\Psi \;{\bar {\Psi }}}{P^{2}-M^{2}}}=S_{1}\,S_{2}+S_{1}\,S_{2}\,K_{12}{\frac {\Psi \;{\bar {\Psi }}}{P^{2}-M^{2}}}$

wobei, setzt man $P^{2}=M^{2}$, beide Seiten von ihren Residuen dominiert werden und man erhält

$\Psi =S_{1}\,S_{2}\,K_{12}\Psi$.

Die ist schon eine Form der Bethe-Salpeter-Gleichung. Oft werden jetzt noch die Bethe-Salpeter-Amplituden Γ eingeführt als

$\Psi =S_{1}\,S_{2}\,\Gamma$

womit man die obige Form der Bethe-Salpeter-Gleichung erhält:

$\Gamma =K_{12}\,S_{1}\,S_{2}\,\Gamma$.

Näherungen

Die Bethe-Salpeter-Gleichung in Leiter-Näherung

Da die Bethe-Salpeter-Gleichung alle möglichen Wechselwirkungen zwischen den zwei Konstituenten beinhaltet ist eine vollständige Lösung nur selten (wenn überhaupt) möglich und in praktischen Rechnungen sind Näherungen nötig.

• Eine Möglichkeit ist, eines der Teilchen als viel schwerer als das andere anzunehmen und dann die Diracgleichung eines (des leichten) Teilchens in einem Potential zu lösen.
• Will man wirklich, im Gegensatz zu oben, die Bethe-Salpeter-Gleichung lösen, so muss man den Wechselwirkungskern modellieren. In Quantenfeldtheorien werden Wechselwirkungen durch Teilchenaustausch beschrieben. Die einfachste Annahme über den Wechselwirkungskern ist nun, dass er genau aus dem Austausch eines dieser Kraftteilchen (z. B. Photonen in der Quantenelektrodynamik, Gluonen in der Quantenchromodynamik), zwischen den zwei Konstituenten besteht, der dann unendlich oft wiederholt wird. Da das entsprechende Feynmandiagramm einer Leiter ähnelt, heißt diese Näherung die Leiter-Näherung (oder Regenbogen-Leiter-Näherung) der Bethe-Salpeter-Gleichung.

Siehe auch

• Dyson-Gleichung
• Dyson-Schwinger-Gleichungen
• Gebundener Zustand

Weblinks

• The Bethe-Salpeter Equation (englisch)