Das 51-Eck oder Pentakontahenagon ist eine geometrische Figur und ein Vieleck (Polygon). Es ist bestimmt durch einundfünfzig Punkte und deren einundfünfzig Verbindungen namens Strecken, Seiten oder Kanten.
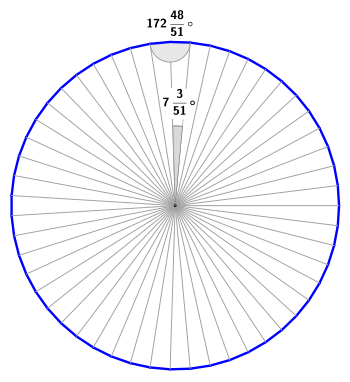
Das – im Folgenden ausschließlich beschriebene – regelmäßige 51-Eck ist ein nicht überschlagenes Polygon mit 51 gleich langen Seiten auf einem gemeinsamen Umkreis. Es ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel ein konstruierbares Polygon, da die Anzahl seiner Seiten als Produkt einer Zweierpotenz mit paarweise voneinander verschiedenen Fermatschen Primzahlen () darstellbar ist.
Dieser Artikel behandelt im Folgenden das regelmäßige 51-Eck.
Größen
Bearbeiten| Größen eines regelmäßigen 51-Ecks | ||
|---|---|---|
| Innenwinkel | ||
| Zentriwinkel
(Mittelpunktswinkel) |
||
| Seitenlänge | ||
| Umkreisradius | ||
| Inkreisradius | ||
| Höhe | ||
| Flächeninhalt | ||
Innenwinkel
BearbeitenDer Innenwinkel wird von zwei benachbarten Seitenkanten eingeschlossen. In der allgemeinen Formel für regelmäßige Polygone steht die Variable für die Anzahl der Eckpunkte des Polygons. In diesem Fall ist für die Variable die Zahl einzusetzen.
Zentriwinkel
BearbeitenDer Zentriwinkel oder Mittelpunktswinkel wird von zwei benachbarten Umkreisradien eingeschlossen. In der allgemeinen Formel ist für die Variable die Zahl einzusetzen.
Seitenlänge und Umkreisradius
BearbeitenDas 51-Eck ist in einundfünfzig gleichschenklige Dreiecke sogenannte Teildreiecke teilbar. Aus der Hälfte eines solchen Teildreiecks, sprich aus einem rechtwinkligen Dreieck mit der Kathete (halbe Seitenlänge) , der Hypotenuse (Umkreisradius) und dem halben Zentriwinkel erhält man mithilfe der Trigonometrie im rechtwinkligen Dreieck die Seitenlänge wie folgt
durch Umformen erhält man den Umkreisradius
Inkreisradius
BearbeitenDer Inkreisradius ist die Höhe eines Teildreiecks, senkrecht zur Seitenlänge des 51-Ecks. Wird zur Berechnung wieder das gleiche rechtwinklige Dreieck wie bei der Seitenlänge verwendet, gilt für den Inkreisradius
Höhe
BearbeitenDie Höhe eines regelmäßigen 51-Ecks ergibt sich aus der Summe von Inkreisradius und Umkreisradius .
Flächeninhalt
BearbeitenDer Flächeninhalt eines Dreiecks berechnet sich allgemein . Für die Berechnung des 51-Ecks werden die Ergebnisse der Seitenlänge und des Inkreisradius herangezogen, worin für die Höhe eingesetzt wird.
- daraus folgt für die Fläche eines Teildreiecks
- zusammengefasst ergibt sich
und für die Fläche des gesamten 51-Ecks
Konstruktion
BearbeitenWie oben in Regelmäßiges 51-Eck beschrieben, ist das 51-Eck als Konstruktion mit Zirkel und Lineal darstellbar. Da sich die Anzahl seiner Ecken aus der Multiplikation der beiden Fermatschen Primzahlen und ergibt, kann das regelmäßige 51-Eck durch eine Erweiterung einer bereits bekannten Konstruktion des Siebzehnecks gefunden werden. Die zwei Polygone Dreieck und Siebzehneck (deren Anzahl der Seiten entspricht den Fermatschen Primzahlen bzw. ) werden im gemeinsamen Umkreis mit einem gemeinsamen Eckpunkt übereinander gelegt, so wie dies z. B. Johannes Kepler in seinem Werk WELT-HARMONIK in der Konstruktion des Fünfzehnecks aufzeigt[1].
Als Basis für die Konstruktion kann prinzipiell eine der drei in Siebzehneck beschriebenen Methoden ausgewählt werden. Aus Gründen des sehr geringen erforderlichen Aufwands wird die Methode von Duane W. DeTemple,[2] aus dem Jahr 1991, verwendet.
Vorüberlegungen
BearbeitenIn der Zeichnung des Siebzehnecks nach Duane W. DeTemple (Bild 1) ist gut erkennbar, die Mittelsenkrechte ab schneidet nicht nur den Kreisbogen sondern auch den Umkreis. Wird dieser Schnittpunkt als markiert, liegt er direkt neben dem Eckpunkt Damit ergibt sich der Zentriwinkel mit der Winkelweite eines gleichseitigen Dreiecks, der quasi zum Zentriwinkel des Siebzehnecks geometrisch im Uhrzeigersinn addiert ist.
Folglich gilt für
- Zentriwinkel des Kreissektors
- Zentriwinkel des Kreissektors
- wegen
- Zentriwinkel des 51-Ecks
- gilt auch
Somit ist die Strecke eine Seitenlänge und ein Eckpunkt des gesuchten 51-Ecks.
Die Position des Eckpunktes des 51-Ecks ergibt sich auch aus der Anzahl der Seitenlängen die im Zentriwinkel enthalten sind
- daraus folgt
- ausgehend von dem nicht mitgezählten Eckpunkt entspricht der im Uhrzeigersinn 17. Eckpunkt dem Eckpunkt der gegen den Uhrzeigersinn abgezählt ist.
Der 17. Eckpunkt des 51-Ecks liegt demnach, bezogen auf die Mittelachse , genau gegenüber dem 34. Eckpunkt.
Konstruktionsbeschreibung
BearbeitenDie, im Vergleich zum Original, geänderten Bezeichner im Bild 2 entsprechen denen der heute üblichen.
- Zeichnen einer Geraden (analytisch eine X-Achse) und bestimmen eines Punktes darauf, den späteren Mittelpunkt des Polygons (analytisch ein Koordinatenursprung).
- Zeichnen eines Kreises als Umkreis (analytisch ein Einheitskreis) um . Es ergeben sich zwei Schnittpunkte, den Eckpunkt des Polygons und der Gegenpunkt .
- Errichten der Senkrechten (analytisch eine Y-Achse) auf der Gerade in . Es ergibt sich der Schnittpunkt .
- Halbierung der Strecke in .
- Errichten der Senkrechte auf der Geraden in . Die beiden Schnittpunkte mit sind die Eckpunkte und des 51-Ecks.
- Zeichnen des Kreisbogens um mit dem Radius . Der Schnittpunkt mit der Senkrechten ist .
- Nun wird um der erste Carlyle-Kreis durch den Punkt gezogen; die Schnittpunkte sind und .
- Die Strecke wird halbiert. Man erhält .
- Zeichnen eines zweiten Carlyle-Kreises um durch . Die Schnittpunkte mit x sind die Punkte und (letzterer nicht eingezeichnet, da er nicht weiter benötigt wird).
- Die Strecke wird halbiert. Man erhält .
- Zeichnen eines dritten Carlyle-Kreises um durch . Die Schnittpunkte mit x sind die Punkte und (letzterer ebenfalls nicht eingezeichnet, da er nicht weiter benötigt wird).
- Abtragen der Strecke auf von aus ab. Man erhält Punkt
- Verbinden der Punkte und mit einer Strecke.
- Halbieren der Strecke . Man erhält Punkt .
- Zeichnen eines vierten Carlyle-Kreises um durch . Die Schnittpunkte mit x sind die Punkte und (letzterer nicht beschriftet, da er nicht weiter benötigt wird).
- Zeichnen eines Kreisbogens um mit dem Umkreisradius . Die Schnittpunkte mit dem Umkreis sind die zwei zu benachbarten Punkte des 17-Ecks und damit die Punkte und des 51-Ecks.
- Durch wiederholtes Abtragen der Strecke auf dem Umkreis , beginnend mit , erhält man die fehlenden Punkte eines regelmäßigen 17-Ecks. Bis hierhin entspricht die Konstruktion der des 17-Ecks.
- Durch wiederholtes Abtragen der Strecke auf dem Umkreis , ausgehend von den Punkten (blau) und (rot), erhält man alle noch fehlenden Eckpunkte des 51-Ecks, welche miteinander zum 51-Eck verbunden werden können.
Vorkommen
BearbeitenArchitektur
Der Querschnitt des RWE-Turms in Essen ist ein regelmäßiges 51-Eck.
Literatur
Bearbeiten- H. Maser: Die Teilung des Kreises ..., Artikel 365., in Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik, Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen; abgerufen am 15. März 2018.
Weblinks
BearbeitenEinzelnachweise
Bearbeiten- ↑ Johannes Kepler: WELT-HARMONIK. XLIV. Satz., Seite des Fünfzehnecks, Seite 44. In: Google Books. R. OLDENBURG VERLAG 2006, übersetzt und eingeleitet von MAX CASPAR 1939, S. 401, abgerufen am 21. Februar 2018.
- ↑ Duane W. DeTemple: Carlyle Circles and the Lemoine Simplicity of Polygon Constructions. ( vom 11. August 2011 im Internet Archive). The American Mathematical Monthly, Vol. 98, No. 2 (Feb., 1991), S. 101–104 (JSTOR:2323939) aufgerufen am 16. Februar 2018.
