Rijndael MixColumns
Der MixColumns-Schritt ist ein Schritt im Rijndael-Algorithmus (AES).
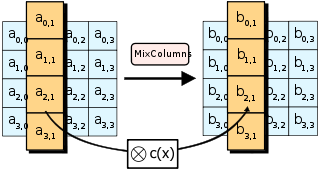
MixColumns Schritt, wird jede Spalte des State mit c(x) verknüpft.Die Matrizenmultiplikation
BearbeitenIn diesem Schritt findet eine Matrizenmultiplikation eines Spaltenvektors des States mit einer MDS-Matrix statt, damit alle 4 Eingabebytes jedes Ausgabebyte beeinflussen.
Die Arithmetik findet allerdings nicht auf den Natürlichen Zahlen statt, sondern auf dem Galois-Körper des Rijndael.
Der Galois-Körper des Rijndael
BearbeitenDer Galois-Körper des Rijndael ist der Galois-Körper .
ist die Menge aller Polynome maximal 7. Grades mit Koeffizienten aus dem Restklassenkörper .
Ein allgemeines Polynom aus besitzt die Form Wie leicht nachzuvollziehen ist, lässt sich jedes dieser Polynome durch ein Byte repräsentieren, wobei jeweils das -te Bit den Koeffizienten repräsentiert.
Die Addition auf ist analog zum Körper als XOR-Verknüpfung definiert, sie findet koeffizientenweise bzw. bitweise statt. Die Subtraktion entspricht der Addition, da die XOR-Verknüpfung ihre eigene Umkehrfunktion ist. Beispiel:
Die Multiplikation( ) findet modulo des irreduziblen Polynoms statt. Hierzu multipliziert man die beiden Polynome und berechnet dann Mittels einer Polynomdivision den Divisionsrest.
Beispiel
BearbeitenBeispielhaft wird nun die Berechnung von mit durchgeführt. Zahlen sind, wenn nicht anders angegeben, hexadezimal.
Daraus folgt
Die Terme sowie sind trivial.
Daraus ergibt sich mit XOR:
Die Umkehrung des MixColumns Schrittes
BearbeitenDie Entschlüsselung kann in diesem Schritt in derselben Weise erfolgen wie die Verschlüsselung. Allerdings muss man hierzu mit der inversen Matrix multiplizieren. Sie lautet (Zahlen hexadezimal):
da
Möglichkeiten zur Implementierung
BearbeitenDadurch, dass im Rijndael bei der Verschlüsselung nur Multiplikationen mit , oder stattfinden, lässt sich der Algorithmus sehr effizient und einfach am Computer implementieren.
Die Multiplikation mit ist trivial. Die Multiplikation mit bedeutet in der Binärdarstellung eine Verschiebung um 1 Bit nach links (die Moduloberechnung muss noch gesondert betrachtet werden), und die Multiplikation mit lässt sich in eine Multiplikation mit und anschließende Addition mit sich selbst aufspalten. Falls ein Überlauf stattfindet, so muss man das Zwischenergebnis noch mit XOR-verknüpfen, um das richtige Ergebnis zu erhalten.
Folgender C-Code dient nur als Beispiel für eine mögliche einfache Implementierung und stellt keine sichere Referenzimplementierung dar.
unsigned char mul123(unsigned char a, unsigned char b) {
if (b==1) {
return a;
}
else if (b==2) {
unsigned char c = a << 1;
if (a & 0x80)
c ^= 0x1b;
return c;
}
else if (b==3) {
return mul123(a, 2) ^ a;
}
else {
exit{EXIT_FAILURE};
}
}
Bei der Entschlüsselung bedarf es allerdings auch der Multiplikation mit anderen Zahlen, wo der obenstehende Ansatz nutzlos wird.
Für geeignetes gilt ist bijektiv. Die Umkehrfunktion heiße . Ein solches geeignetes nennt man einen Generator, Beispiele hierfür wären die 3 oder die 5, es gibt allerdings noch einige weitere.
Beweis: Da endlich, lässt sich das durch nachrechnen überprüfen.
Da bijektiv ist, gilt für :
Für gilt
Erzeugen wir uns nun für die Multiplikation eine Exponential- und Logarithmustabelle für einen Generator, so können wir mit Hilfe dieser die allgemeine Multiplikation auf effektiv implementieren. Die Tabelle kann entweder zur Laufzeit berechnet werden – mit obiger Funktion bietet sich der Generator 3 an – oder im Quellcode vorliegen.
unsigned char RijndaelGaloisMul(unsigned char a, unsigned char b){
if(a && b) //falls a != 0 und b != 0
return exp_table[(ln_table[a] + ln_table[b]) % 0xff];
else
return 0;
}
Nachfolgend die Exponential- und Logarithmustabelle für den Generator 3:
Potenzen: | *0 *1 *2 *3 *4 *5 *6 *7 *8 *9 *a *b *c *d *e *f | ---------------------------------------------------------------------- 0*| 01 03 05 0f 11 33 55 ff 1a 2e 72 96 a1 f8 13 35 |0* 1*| 5f e1 38 48 d8 73 95 a4 f7 02 06 0a 1e 22 66 aa |1* 2*| e5 34 5c e4 37 59 eb 26 6a be d9 70 90 ab e6 31 |2* 3*| 53 f5 04 0c 14 3c 44 cc 4f d1 68 b8 d3 6e b2 cd |3* 4*| 4c d4 67 a9 e0 3b 4d d7 62 a6 f1 08 18 28 78 88 |4* 5*| 83 9e b9 d0 6b bd dc 7f 81 98 b3 ce 49 db 76 9a |5* 6*| b5 c4 57 f9 10 30 50 f0 0b 1d 27 69 bb d6 61 a3 |6* 7*| fe 19 2b 7d 87 92 ad ec 2f 71 93 ae e9 20 60 a0 |7* 8*| fb 16 3a 4e d2 6d b7 c2 5d e7 32 56 fa 15 3f 41 |8* 9*| c3 5e e2 3d 47 c9 40 c0 5b ed 2c 74 9c bf da 75 |9* a*| 9f ba d5 64 ac ef 2a 7e 82 9d bc df 7a 8e 89 80 |a* b*| 9b b6 c1 58 e8 23 65 af ea 25 6f b1 c8 43 c5 54 |b* c*| fc 1f 21 63 a5 f4 07 09 1b 2d 77 99 b0 cb 46 ca |c* d*| 45 cf 4a de 79 8b 86 91 a8 e3 3e 42 c6 51 f3 0e |d* e*| 12 36 5a ee 29 7b 8d 8c 8f 8a 85 94 a7 f2 0d 17 |e* f*| 39 4b dd 7c 84 97 a2 fd 1c 24 6c b4 c7 52 f6 01 |f*
Logarithmen: | *0 *1 *2 *3 *4 *5 *6 *7 *8 *9 *a *b *c *d *e *f | ---------------------------------------------------------------------- 0*| -- 00 19 01 32 02 1a c6 4b c7 1b 68 33 ee df 03 |0* 1*| 64 04 e0 0e 34 8d 81 ef 4c 71 08 c8 f8 69 1c c1 |1* 2*| 7d c2 1d b5 f9 b9 27 6a 4d e4 a6 72 9a c9 09 78 |2* 3*| 65 2f 8a 05 21 0f e1 24 12 f0 82 45 35 93 da 8e |3* 4*| 96 8f db bd 36 d0 ce 94 13 5c d2 f1 40 46 83 38 |4* 5*| 66 dd fd 30 bf 06 8b 62 b3 25 e2 98 22 88 91 10 |5* 6*| 7e 6e 48 c3 a3 b6 1e 42 3a 6b 28 54 fa 85 3d ba |6* 7*| 2b 79 0a 15 9b 9f 5e ca 4e d4 ac e5 f3 73 a7 57 |7* 8*| af 58 a8 50 f4 ea d6 74 4f ae e9 d5 e7 e6 ad e8 |8* 9*| 2c d7 75 7a eb 16 0b f5 59 cb 5f b0 9c a9 51 a0 |9* a*| 7f 0c f6 6f 17 c4 49 ec d8 43 1f 2d a4 76 7b b7 |a* b*| cc bb 3e 5a fb 60 b1 86 3b 52 a1 6c aa 55 29 9d |b* c*| 97 b2 87 90 61 be dc fc bc 95 cf cd 37 3f 5b d1 |c* d*| 53 39 84 3c 41 a2 6d 47 14 2a 9e 5d 56 f2 d3 ab |d* e*| 44 11 92 d9 23 20 2e 89 b4 7c b8 26 77 99 e3 a5 |e* f*| 67 4a ed de c5 31 fe 18 0d 63 8c 80 c0 f7 70 07 |f*