Komposition (Mathematik)
Der Begriff Komposition bedeutet in der Mathematik meist die Hintereinanderschaltung von Funktionen, auch als Verkettung, Verknüpfung oder Hintereinanderausführung bezeichnet. Sie wird meist mit Hilfe des Verkettungszeichens notiert.
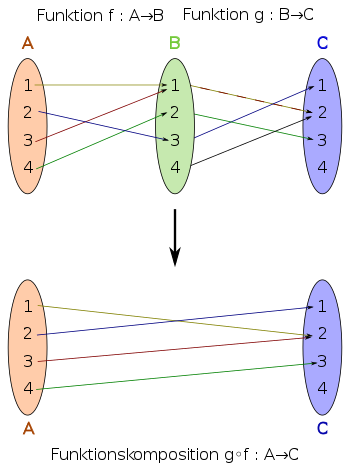
Die Darstellung einer Funktion als Verkettung zweier oder mehrerer, im Allgemeinen einfacherer Funktionen ist zum Beispiel in der Differential- und Integralrechnung wichtig, wenn es darum geht, Ableitungen mit der Kettenregel oder Integrale mit der Substitutionsregel zu berechnen.
Der Begriff Komposition kann von Funktionen auf Relationen und partielle Funktionen verallgemeinert werden.
Definition
BearbeitenSeien beliebige Mengen und sowie Funktionen, so heißt die Funktion
die Komposition von und . Der Ausdruck „ “ wird als „ verknüpft mit “, „ komponiert mit “, „ nach “ oder „ Kringel “ gelesen.[1][2][3] Es ist dabei zu beachten, dass die zuerst angewandte Abbildung rechts steht, im Gegensatz zum Diagramm, wo sie links steht:
Abweichende Schreibweisen
BearbeitenEine alternative Schreibweise für ist , wobei man dies nicht mit dem Produkt der Funktionen verwechseln darf, bei dem das Multiplikationszeichen ebenfalls oft weggelassen wird.
Es gibt auch wenige Autoren, die nach als mit schreiben, die Funktionen also von links nach rechts auswerten. Welche Reihenfolge gewählt wurde, lässt sich oft an einem Beispiel des Autors nachvollziehen. Daneben existiert auch die Notation, bei der das Funktionssymbol rechts vom Argument geschrieben wird, also (oder auch ) anstelle von . Dann ist die Auswertung von links nach rechts naheliegend, also (hauptsächlich im Kontext von (rechten) Gruppenoperationen verbreitet).
Beispiele
BearbeitenMan betrachte die folgenden Funktionen, für die als Definitions- und Wertemenge die Menge der reellen Zahlen oder eine Teilmenge davon angenommen wird. Ist die Funktion durch und die Funktion durch gegeben, so ergibt die Verkettung von und die Funktion mit
- .
Umgekehrt lässt sich die durch definierte Funktion als darstellen, wobei
sind.
Eigenschaften
BearbeitenAssoziativität
BearbeitenDie Komposition von Funktionen ist assoziativ. Kommt nämlich zu den obigen Funktionen und noch eine Funktion hinzu, dann definiert sowohl
wie
eine Funktion , die beide dieselben Werte produzieren, es gilt also:
für alle ; mit der Folge, dass die Klammern weggelassen werden können. Recht eigentlich ist diese Assoziativität nur eine notationelle Angelegenheit, denn die Auswertungsreihenfolge ist in beiden Fällen dieselbe: sie ist im Ausdruck formuliert und beginnt immer bei der innersten Klammer , rechts mit der Anwendung von auf den Operanden und schreitet nach links fort.
Identische Abbildungen
BearbeitenDie identische Abbildung verhält sich bei der Komposition neutral, für eine Funktion gilt also:
- ,
wobei und die jeweiligen Identitäten auf den Mengen und darstellen.
Injektivität, Surjektivität, Bijektivität
BearbeitenWichtige Eigenschaften, die eine Funktion besitzen kann, sind
- Injektivität (kein Element in wird mehrfach angenommen),
- Surjektivität (jedes Element in wird angenommen),
- Bijektivität (jedes Element in wird angenommen, und keins wird mehrfach angenommen).
Jede dieser Eigenschaften überträgt sich auf die Verkettung, es gilt also:
- Die Komposition injektiver Funktionen ist injektiv.
- Die Komposition surjektiver Funktionen ist surjektiv.
- Die Komposition bijektiver Funktionen ist bijektiv.
Umgekehrt gilt: Ist eine Verkettung
- injektiv, so ist injektiv.
- surjektiv, so ist surjektiv.
- bijektiv, so ist injektiv und surjektiv.
Kommutativität
BearbeitenAuch wenn Definitions- und Wertemenge jeweils übereinstimmen, ist die Komposition von Funktionen normalerweise nicht kommutativ. Beispielsweise gilt für die Funktionen und :
Iterationen kommutieren generell, so auch die Identität und die Umkehrfunktion, so vorhanden. Ansonsten kommt eine kommutative Komposition nur bei ganz speziell gewählten Kombinationen von Funktionen vor. Beispiele dazu mit als Definitions- und Wertemenge:
- und ergeben
- und ergeben
- und ergeben
Iteration
BearbeitenIst eine Abbildung einer Menge in sich selbst, dann kann man diese Funktion mit sich selbst verketten und erhält die Funktion , die wiederum eine Funktion ist. Wie bei assoziativen Operationen üblich kann nun induktiv für jede natürliche Zahl die -te Iteration von erklärt werden durch:
Außerdem setzt man
- ,
mit der identischen Abbildung als dem neutralen Element der Verkettung.
wird als -te Iterierte (oft auch als -te Potenz) von bezeichnet.
Falls auf eine Multiplikation definiert ist, darf die Iteration (der Verkettung) nicht mit der Exponentiation (Iteration der Multiplikation) verwechselt werden: kann in diesem Fall auch den Ausdruck bezeichnen (siehe dazu auch den § Abgrenzung der Schreibungen).
Ist bijektiv, dann existiert die Umkehrfunktion , und die negativen Iterationen sind definiert durch:
Beispiele
BearbeitenSei die Menge der positiven reellen Zahlen und gegeben durch . Dann gilt:
Algebraische Strukturen
BearbeitenWird die Menge aller Funktionen aus einer gegebenen Menge in sich selbst betrachtet, so definiert die Komposition eine innere zweistellige Verknüpfung auf , bezüglich der (mit der identischen Abbildung als neutralem Element) ein Monoid ist.
Werden nur bijektive Funktionen herangezogen, ist das Monoid sogar eine Gruppe mit der jeweiligen Umkehrfunktion als inversem Element. Ist dann die Menge endlich mit Elementen ist, handelt es sich um die symmetrische Gruppe .
Strukturverträgliche Abbildungen
BearbeitenIn der Mathematik betrachtet man oft Mengen mit einer zusätzlichen Struktur sowie Abbildungen, die mit dieser Struktur verträglich sind, zum Beispiel
- lineare Abbildungen zwischen Vektorräumen
- stetige Abbildungen zwischen topologischen Räumen
- Gruppenhomomorphismen zwischen Gruppen
Wünschenswert ist nun, dass die Strukturverträglichkeit bei der Komposition erhalten bleibt, und in der Tat gilt in den Beispielen:
- Die Komposition linearer Abbildungen ist linear.
- Die Komposition stetiger Abbildungen ist stetig.
- Die Komposition von Gruppenhomomorphismen ist ein Gruppenhomomorphismus.
Diese Überlegungen führen zur Kategorientheorie, bei der man sogar davon abstrahiert, dass es sich um Abbildungen handelt, und nur noch die Assoziativität sowie die Eigenschaft der Identitäten für die Komposition fordert.
Komposition von Relationen
BearbeitenZu einer Funktion ist der Funktionsgraph eine Relation . Bezüglich der Komposition von Funktionen gilt dann (unter Verwendung der Infixnotation):
- .
Diese Beobachtung führt zur Definition der Komposition von zweistelligen Relationen und : Die Relation ist gegeben durch
- .
Bei der Komposition von Relationen wird also immer die Reihenfolge von rechts nach links eingehalten.
Beispiel
Bearbeitensei die Menge der Punkte, die Menge der Geraden und die Menge der Ebenen im dreidimensionalen Raum. Die Relationen und seien festgelegt durch:
- der Punkt liegt auf der Geraden
- die Gerade ist in der Ebene enthalten
Für die Komposition gilt dann:
- der Punkt liegt in der Ebene
Eigenschaften
Bearbeiten- Die Komposition von Relationen ist assoziativ.
- Bezeichnet die identische Relation auf einer Menge , also die Menge aller Paare , dann gilt für jede Relation :
- Ist eine Relation auf einer Menge , dann sind also auch alle Potenzen (mit ) definiert. Diese Potenzen werden zum Beispiel bei der Definition der reflexiv-transitiven Hülle verwendet. Eine Relation mit heißt transitiv.
Abweichende Notation in der Physik
BearbeitenIn der Physik und anderen Naturwissenschaften ist es üblich, die Verkettung einer Funktion mit der "äußeren Funktion" zu identifizieren: . Aufgrund dieser Notation entstehen in physikalischer Literatur teilweise Gleichungen, die auf den ersten Blick nach gängigen mathematischen Konventionen falsch oder sinnlos sind, etwa
- ,
wobei der Ortsvektor des Punktes ist und seine euklidische Länge. Diese Gleichung ist, mathematisch gesehen, im Prinzip falsch, da nach der linken Seite der Gleichung eine Funktion darstellt (setzt man doch in ein Element ein), auf der rechten Seite offenbar als Definitionsbereich eine Teilmenge der reellen Zahlen aufweist, also , da man in die skalare Größe einsetzt. Gemeint ist mit dieser intuitiven Gleichung jedoch, dass (für einen betrachteten Spezialfall) die physikalische Größe (in diesem Fall ein Potential), das im Allgemeinen eine Funktion des Ortes ist, mit einer Funktion beschrieben werden kann, die nur vom Abstand des Ortes vom Nullpunkt abhängt. Eine mathematisch „saubere“ Formulierung dieser Aussage würde etwa lauten:
ist also eine Verkettung aus der skalaren Funktion und der euklidischen Norm :
- .
Wir erhalten die obige, intuitive Schreibweise dieser Gleichung, indem wir zunächst die Verkettung symbolisch mit der äußeren Funktion identifizieren und diese wiederum mit dem Potenzial . Vorteile der Notation sind intuitiv verständliche Schreibweisen und eine geringe Anzahl von verschiedenen Symbolen. Ein typisches Beispiel einer Funktion, die die obige Gleichung erfüllt, sind Zentralpotenziale der Form
die u. a. in der Elektrostatik verwendet werden. ist in diesem Fall eine Verkettung der skalaren Funktion mit
mit der euklidischen Norm:
Literatur
Bearbeiten- Composition. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
