Benutzer:Schojoha/Spielwiese/Eigene Beweise

Ein Supremumsprinzip im Zusammenhang mit drei Sätzen von Krein–Milman, Klee–Straszewicz und Bauer

Im Zusammenhang mit den Sätzen von Krein-Milman und Klee–Straszewicz ergibt sich die Frage, ob ein dem Maximumprinzip von Bauer analoges Prinzip auch für konvexe unterhalbstetige Funktionen gelten kann. Wie sich zeigen lässt, hat ein solches in einem sehr allgemeinen Rahmen Gültigkeit. Es handelt sich um das im Folgenden dargestellte Supremumsprinzip.

Formulierung des Supremumsprinzips

Gegeben sei ein Vektorraum $X$ über dem Körper $\mathbb {R}$ der reellen Zahlen, der zugleich ein topologischer Raum sein soll mit ${\mathcal {O}}\subseteq 2^{X}$ als Topologie, wobei bzgl. ${\mathcal {O}}$ die Bildung des topologischen Abschlusses (wie üblich) in der Form $A\mapsto {\overline {A}}\;(A\subseteq X)$ angezeigt wird.

Weiter gegeben seien hier zwei nichtleere Teilmengen $E$ und $T$ sowie eine numerische Funktion $\phi \colon T\to ]-\infty ,+\infty ]$, welche $T$ in die um $+\infty$ erweiterten reellen Zahlen abbilden soll.

Dabei soll $T={\overline {\operatorname {conv} \left(E\right)}}$ sein und $\phi$ sowohl konvex als auch bzgl. ${\mathcal {O}}$ unterhalbstetig.

Dann gilt:

(SP) $\sup _{x\in T}{\phi (x)}=\sup _{x\in E}{\phi (x)}$.

Folgerungen

Bei Berücksichtigung der Sätze von Krein-Milman und Klee–Straszewicz gewinnt man durch Anwendung des Supremumsprinzips sofort folgendes Korollar:

Korollar 1a

Gegeben seien ein Hausdorff'scher lokalkonvexer topologischer $\mathbb {R}$-Vektorraum $X$ und darin eine nichtleere Teilmenge $T\subset X$ sowie eine numerische Funktion $\phi \colon T\to ]-\infty ,+\infty ]$.

$T$ sei kompakt und konvex und $\phi$ sei konvex und unterhalbstetig.

Dann gilt:

(I_1a1) $\sup _{x\in T}{\phi (x)}=\sup _{x\in {\operatorname {ext} {T}}}{\phi (x)}$ .

Ist dabei $X$ ein normierter $\mathbb {R}$-Vektorraum, so gilt sogar:

(I_1a2) $\sup _{x\in T}{\phi (x)}=\sup _{x\in {\operatorname {exp} {T}}}{\phi (x)}$ .

Verschärft man das Supremumsprinzip in anderer Weise, indem man nämlich sogar Kompaktheit für die kleinere Teilmenge sowie für die Funktion Stetigkeit statt Unterhalbstetigkeit annimmt und den Weierstraß'schen Satz vom Maximum einbezieht, so gewinnt man ein anderes Korollar:

Korollar 1b

Gegeben seien (wie oben) ein $\mathbb {R}$-Vektorraum $X$ mit Topologie ${\mathcal {O}}$ und darin zwei Teilmengen $E$ und $T$ mit $\emptyset \neq E\subseteq T\subseteq X$ und weiter eine numerische Funktion $\phi \colon T\to ]-\infty ,+\infty ]$.

Dabei sei $E$ kompakt (oder auch lediglich quasikompakt!) und es gelte $T={\overline {\operatorname {conv} \left(E\right)}}$, während $\phi$ sowohl konvex als auch stetig sein soll.

Dann gibt es einen Raumpunkt $e_{0}\in E$ mit

(I_1b) $\phi (e_{0})=\max _{x\in T}{\phi (x)}$ .

Bei Anwendung des Supremumsprinzips auf den Fall eines mit der diskreten Topologie versehenen Vektorraums gewinnt man ein noch das folgende allgemeine Ergebnis, das dann unabhängig von allen topologischen Betrachtungen Gültigkeit hat:

Korollar 1c

Gegeben seien ein $\mathbb {R}$-Vektorraum $X$ und darin zwei nichtleere Teilmengen $E$ und $T$ sowie eine numerische Funktion $\phi \colon T\to ]-\infty ,+\infty ]$.

Ist weiter $T=\operatorname {conv} {E}$ und zudem $\phi$ konvex, so gilt:

(I_1c) $\sup _{x\in T}{\phi (x)}=\sup _{x\in E}{\phi (x)}$ .

Verknüpft man Korollar 1a und Korollar 1b, so führt dies zu einem weiteren Korollar:

Korollar 2

Gegeben seien ein Hausdorff'scher lokalkonvexer topologischer $\mathbb {R}$-Vektorraum $X$ und darin eine nichtleere sowohl kompakte als auch konvexe Teilmenge $T\subset X$ sowie eine sowohl konvexe als auch stetige numerische Funktion $\phi \colon T\to ]-\infty ,+\infty ]$.

Dann gibt es einen Extremalpunkt $e_{0}\in {\overline {\operatorname {ext} {T}}}$ mit

(I_21) $\phi (e_{0})=\max _{x\in T}{\phi (x)}$ .

Ist dabei $X$ ein normierter $\mathbb {R}$-Vektorraum, so gibt es sogar einen exponierten Raumpunkt $e_{0}\in {\overline {\operatorname {exp} {T}}}$ mit

(I_22) $\phi (e_{0})=\max _{x\in T}{\phi (x)}$ .

Naheliegend ist nun die Frage, was sich bei Anwendung des Supremumsprinzips im euklidischen Raum ergibt. Man erhält hier:

Korollar 3

Gegeben seien im euklidischen Raum $\mathbb {R} ^{n};(n\in \mathbb {N} )$ eine offenes konvexes Gebiet $U\subseteq \mathbb {R} ^{n}$ und darin ein nichtleeres beschränktes konvexes Polyeder $T\subseteq U$ sowie ein konvexes Funktional $\phi \colon T\to \mathbb {R}$.

Dann besitzt $T$ einen Eckpunkt $e_{0}$, auf dem $\phi$ sein Maximum annimmt.

Beweise

Zum Supremumsprinzip

Es sind für den Nachweis von (SP) die Ungleichungen $\geq$ und $\leq$ zu zeigen. Da erstere offensichtlich wahr ist, bleibt lediglich die entgegengesetzte Ungleichung $\leq$ herzuleiten.

Dazu sei $s=\sup _{x\in E}{\phi (x)}$ und $K={\phi }^{-1}\left([-\infty ,s]\right)$, also die Menge aller Elemente von $T$, deren $\phi$-Bilder $s$ nicht übersteigen.

Nach Voraussetzung ist $T$ in $X$ der Abschluss der konvexen Hülle von $E$. Also bleibt wegen $E\subseteq K$ lediglich zu zeigen, dass auch $K$ sowohl konvex als auch abgeschlossen in $X$ ist. Denn damit hat man $\operatorname {conv} \left(E\right)\subseteq K$ und dann $T\subseteq K$ und folglich für die $x\in T$ stets $\phi (x)\leq s$.

Wegen der Unterhalbstetigkeit von $\phi$ und nach Definition ist $K$ offenbar abgeschlossen in $X$.

Um noch die Konvexität von $K$ nachzuweisen, seien $x,y\in K$ zwei beliebige $K$-Raumpunkte und dazu $r$ eine reelle Zahl mit $0<r<1$. Infolge der Konvexität von $\phi$ hat man die Ungleichung $\phi \left(rx+(1-r)y\right)\leq r\phi (x)+(1-r)\phi (y)$ und damit auch die Ungleichung $\phi \left(rx+(1-r)y\right)\leq rs+(1-r)s=s$. Also liegt mit je zwei Raumpunkten $x$ und $y$ auch jeder Raumpunkt zwischen $x$ und $y$ in $K$. Folglich ist $K$ konvex und alles ist gezeigt.

Zu Korollar 2

Ad (I_21)

Hier gelten die Inklusionen

$T={\overline {\operatorname {conv} \left(\operatorname {ext} {T}\right)}}\subseteq {\overline {\operatorname {conv} \left({\overline {\operatorname {ext} {T}}}\right)}}\subseteq {\overline {\operatorname {conv} \left({\overline {T}}\right)}}={\overline {\operatorname {conv} {\left(T\right)}}}={\overline {T}}=T$

und folglich

$T={\overline {\operatorname {conv} \left({\overline {\operatorname {ext} {T}}}\right)}}$ .

Also ist, da ${\overline {\operatorname {ext} {T}}}$ als abgeschlossenen Teilmenge der kompakten Menge $T$ selbst kompakt ist, alles gezeigt.

Ad (I_22)

Hier kommt mit dem Satz von Klee–Straszewicz noch die Identität ${\overline {\operatorname {ext} {T}}}={\overline {\operatorname {exp} {T}}}$ zur Geltung.

Zu Korollar 3

Hier ist zu berücksichtigen, dass ein im euklidischen Raum gelegenes nichtleeres beschränktes konvexes Polyeder nach einem klassischen Lehrsatz − der auf Hermann Minkowski, Ernst Steinitz und Hermann Weyl zurückgeht !− stets die konvexe Hülle seiner Ecken ist. Also folgt die Behauptung mit Korollar 1c.

Literatur

• Alexander Barvinok: A course in Convexity (= Graduate Studies in Mathematics. Band 54). American Mathematical Society, Providence, Rhode Island 2002, ISBN 0-8218-2968-8 (MR1940576). 
• Philippe Blanchard, Erwin Brüning: Direkte Methoden der Variationsrechnung. Ein Lehrbuch. Springer Verlag, Wien, New York 1982, ISBN 3-211-81692-5 (MR0687073). 
• Philippe G. Ciarlet: Linear and Nonlinear Functional Analysis with Applications. Society for Industrial and Applied Mathematics, Philadelphia, PA 2013, ISBN 978-1-61197-258-0 (MR3136903). 
• Bernhard Korte, Jens Vygen: Kombinatorische Optimierung : Theorie und Algorithmen (= Masterclass). 3. Auflage. Springer Spektrum, Berlin 2018, ISBN 978-3-662-57690-8. 
• Kurt Leichtweiß: Konvexe Mengen (= Hochschultext). Springer-Verlag, Berlin, Heidelberg, New York 1980, ISBN 3-540-09071-1 (MR0586235). 
• Jürg T. Marti: Konvexe Analysis (= Lehrbücher und Monographien aus dem Gebiet der Exakten Wissenschaften, Mathematische Reihe. Band 54). Birkhäuser Verlag, Basel, Stuttgart 1977, ISBN 3-7643-0839-7 (MR0511737). 
• Jan van Tiel: Convex Analysis: An Introductory Text. John Wiley & Sons, Inc., New York 1984, ISBN 0-471-90263-2 (MR0743904). 
• Günter M. Ziegler: Lectures on Polytopes (= Graduate Texts in Mathematics. Band 152). Springer-Verlag,, New York 1995, ISBN 0-387-94365-X (MR1311028). 

Einzelnachweise

rreferences />

Charakteristikum unendlicher Mengen

In einer Arbeit aus dem Jahre 1952 behandelt der Mathematiker Jürgen Schmidt die Frage, wie sich die in der Algebra auftretenden Hüllenoperatoren und die zugehörigen Hüllensysteme ordnungs- und mengentheoretisch beschreiben lassen. Er formuliert dabei den folgenden Hauptsatz über algebraische Hüllensysteme:

Ein Hüllensystem ist algebraisch genau dann, wenn es induktiv ist.

Bei der Herleitung dieses Hauptsatzes benutzt er an entscheidender Stelle den folgenden Hilfssatz:

Jede unendliche Menge $P$ ist darstellbar als Vereinigungsmenge einer Inklusionskette ${\mathcal {K}}$, deren Mengen $K\in {\mathcal {K}}$ allesamt eine Mächtigkeit haben, welche stets echt kleiner ist als die Mächtigkeit von $P$ selbst.

Dieser Hilfssatz ist, wie sich zeigen lässt und was hier gezeigt wird, auf direktem Wege unter Anwendung des zornschen Lemmas herleitbar.

Beweisschritt I

Wir setzen

$\Sigma :=\{S\subseteq P:|S|<|P|\}$

und zeigen, dass die teilweise geordnete Menge $(\Sigma ,\subseteq )$ nicht induktiv ist.

Nimmt man nämlich – im Widerspruch dazu! – die Induktivität von $(\Sigma ,\subseteq )$ als gegeben an, so folgt durch Anwendung des zornschen Lemmas, dass es in $\Sigma$ ein maximales Element $M$ geben muss. Wegen $|M|<|P|$ muss dann auch $M\subsetneq P$ gelten und man hat ein Element $p\in {P\setminus M}$. Aus Maximalitätsgründen folgt $|M\cup \{p\}|=|P|$. Also ist auch $M$ unendlich und man gewinnt die Gleichung $|M|=|M|+1=|M\cup \{p\}|=|P|$. Damit gilt $|M|<|P|$ und zugleich $|M|=|P|$, was in sich widersprüchlich ist.

Beweisschritt II

Es ist also $(\Sigma ,\subseteq )$ nicht induktiv und damit gibt es eine $\subseteq$-Kette ${\mathcal {L}}$, welche die Gleichung

$|{\bigcup {\mathcal {L}}}|=|P|$

erfüllt. Es existiert folglich eine bijektive Abbildung $f\colon {\bigcup {\mathcal {L}}}\to P$.

Zu diesem setzen wir nun

${\mathcal {K}}:=\{f(L):L\in {\mathcal {L}}\}$

Hierzu gilt nun

1. $\forall L\in {\mathcal {L}}:|f(L)|=|L|<|P|$

und

2. $\bigcup {\mathcal {K}}=\bigcup _{L\in {\mathcal {L}}}{f(L)}=f\left(\bigcup _{L\in {\mathcal {L}}}{L}\right)=P$

und alles ist gezeigt.

Charakteristische Eigenschaft

Dass der genannte Hilfssatz tatsächlich eine charakteristische Eigenschaft unendlicher Mengen angibt, also für eine endliche Menge $F$ nie gilt, sieht man wie folgt:

Für eine solche endliche Menge $F$ ist stets auch die Potenzmenge $2^{F}$ endlich. Folglich gilt dies auch für jede Inklusionskette von echten $F$-Teilmengen. Somit wird man als Vereinigungsmenge einer solchen stets nur die größte der in dieser Inklusionskette enthaltenen $F$-Teilmengen erhalten, welche gemäß Voraussetzung von einer Mächtigkeit echt kleiner als die der endlichen Menge $F$ selbst sein muss.

Literatur

• Jürgen Schmidt: Über die Rolle der transfiniten Schlussweisen in einer allgemeinen idealtheorie. In: Mathematische Nachrichten. Band 7, 1952, S. 165–182. 

Einzelnachweise und Fußnoten

rreferences />

Erklärungsversuch zu einer ramanujanschen Bruchnäherung zur Kreiszahl π

Einleitung

Auf den indischen Mathematiker Srinivasa Ramanujan geht folgende sehr gute - nämlich auf 8 korrekte Nachkommastellen genaue - Näherung der Kreiszahl zurück:

$\pi \approx {\sqrt[{4\,}]{9^{2}+{\frac {19^{2}}{22}}}}$

Wie Arndt und Haenel schreiben, macht Ramanujan hinsichtlich dieser Näherung die dürftige, nicht weiter ausführlich gemachte Angabe, er habe sie empirisch gefunden. Bei der Suche nach einer Erklärung, was Ramanujan unter dem Wort empirisch verstanden haben mag und wie er die Näherung fand, schlagen Arndt und Haenel als naheliegendste Erklärung vor, einen Ansatz via Kettenbrüchen zu versuchen, da Ramanujan ein Experte in Kettenbrüchen war.

Nun zeigt eine leichte Rechnung, dass

$9^{2}+{\frac {19^{2}}{22}}={\frac {2143}{22}}=97+{\frac {9}{22}}$

ist.

Es kann damit dargestellt werden, dass auch eine andere und leichter nachvollziehbare Erklärung zu finden ist, die im Wesentlichen mit periodischen Dezimalbrüchen auskommt. Diese soll im Folgenden beschrieben werden. Dabei wird vorausgesetzt, dass man die ersten 10 Nachkommastellen der Kreiszahl exakt kennt.

Darstellung der Erklärung

Es gibt zwei naheliegende Ansätze:

Ansatz 1

Es ist

${\pi }^{4}=97{,}4090910340\ldots \approx 97{,}4{\overline {09}}$   .

Also ist

$10\cdot {\pi }^{4}\approx 974{,}{\overline {09}}$

und

$1000\cdot {\pi }^{4}\approx 97409{,}{\overline {09}}$   .

Damit ist

$990\cdot {\pi }^{4}\approx 96435$

und folglich

${\pi }^{4}\approx {\frac {96435}{990}}={\frac {45\cdot 2143}{45\cdot 22}}={\frac {2143}{22}}=97+{\frac {9}{22}}$   .

Also hat man die auf 8 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\sqrt[{4\,}]{\frac {2143}{22}}}={\sqrt[{4\,}]{97+{\frac {9}{22}}}}$   .

Ansatz 2

Noch augenfälliger - und insofern ein noch besseres Argument für obige Vermutung hinsichtlich eines Ramanujan'schen Ansatzes mit periodischen Dezimalbrüchen - ist die Angelegenheit, wenn man gleich den Bruch

${\frac {1}{{\pi }^{4}-97}}=2{,}4444436980597\ldots \approx 2{,}{\overline {4}}={\frac {22}{9}}$

zugrundelegt.

Durch Auflösen nach $\pi$ gewinnt man dann unmittelbar die (oben erwähnte) auf 8 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\sqrt[{4\,}]{\frac {2143}{22}}}$   .

Weitere Näherungen ähnlicher Art

Zur Kreiszahl

I

Wie Arndt und Haenel schreiben, hat ein anderer $\pi$-Forscher namens Dario Castellanos eine ähnliche Näherung im Stile Ramanujans angegeben, welche auf der fünften Wurzel basiert. Diese gewinnt man durch die folgende Rechnung: Es ist

${\frac {1}{{\pi }^{5}-306}}=50{,}8006\ldots \approx 50{,}8={\frac {254}{5}}$   .

Also ergibt sich sofort mittels Bruchrechnung und Wurzelziehen die auf 8 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\sqrt[{5\,}]{\frac {77729}{254}}}$   .

II

IIa

Geht man von der (schon lange bekannten) Näherung

$\pi \approx {\frac {22}{7}}$

aus , so ergibt sich (mittels Kehrwertbildung) zunächst - wie oben!-

${\frac {1}{22-7\cdot \pi }}=112{,}976160846789\ldots \approx 113$   .

Daraus ergibt sich die auf 6 korrekte Nachkommastellen genaue (und ebenfalls schon lange bekannte) Näherungsdarstellung

$\pi \approx {\frac {22-{\frac {1}{113}}}{7}}={\frac {2485}{113\cdot 7}}={\frac {355}{113}}$   .

IIb

Verfährt man in gleicher Weise mit der dritten Potenz, so gewinnt man zunächst

${\frac {1}{\left(22-7\cdot \pi \right)^{3}}}=1441983{,}98619987\ldots \approx 1441984=64\cdot 22531$

und dann die auf 10 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\frac {22-{\tfrac {1}{4\cdot {\sqrt[{3\,}]{22531}}}}}{7}}=3{,}1415926535\ldots$   .

IIc

Geht man jedoch von der (auch schon lange bekannten) Näherung

$\pi \approx {\frac {333}{106}}$

aus und verfährt wie zuletzt, wenn auch nun wieder mit der zweiten Potenz, so ergibt sich zunächst

${\frac {1}{\left(106\pi -333\right)^{2}}}=12850{,}994394201\ldots \approx 12851$   .

Daraus ergibt sich die (ebenfalls!) auf 10 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\frac {333+{\tfrac {1}{\sqrt {12851}}}}{106}}=3{,}1415926535\ldots$   .

III

Es ist

${\frac {1}{{\pi }^{2}+1}}=0{,}091999668350\ldots \approx 0{,}092={\frac {23}{250}}$   .

Also ergibt sich - in ähnlicher Weise wie oben - die auf 4 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\sqrt {{\frac {250}{23}}-1}}={\sqrt {\frac {227}{23}}}={\sqrt {10-{\frac {3}{23}}}}={\sqrt {9+{\frac {20}{23}}}}$   .

IV

IVa

Es ist

$\left({\frac {1}{7-{\frac {1}{\ln {\pi }-1}}}}\right)^{2}=121{,}888855131641\ldots \approx 121{,}{\overline {8}}={\frac {1097}{9}}$   .

Also ergibt sich die auf 9 korrekte Nachkommastellen genaue Näherungsdarstellung

$\ln {\pi }\approx 1+{\frac {1}{7-{\frac {3}{\sqrt {1097}}}}}\approx 1,1447298855866\ldots$   .

IVb

Es ist

$({\ln }{\pi })^{64}=5714{,}69898450436\ldots \approx {\frac {1}{10}}\cdot 57146{,}{\overline {98}}={\frac {1}{10}}\cdot (57146+{\frac {98}{99}})$   .

Also ist

$({\ln }{\pi })^{64}\approx {\frac {1}{5}}\cdot ({\frac {28573\cdot 99+49}{99}})={\frac {2828776}{495}}=5714+{\frac {346}{495}}$   .

und es ergibt sich die auf 9 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx \mathrm {e} ^{\sqrt[{64\,}]{\frac {2828776}{495}}}=\mathrm {e} ^{\sqrt[{64\,}]{5714+{\frac {346}{495}}}}$   .

V

Es ist

$\left(\pi -1\right)^{3}=9{,}82224\ldots \approx 9{,}8{\overline {2}}={\frac {1}{10}}\left(98+{\frac {2}{9}}\right)={\frac {442}{45}}$   .

Also ergibt sich - ähnlich wie oben - die auf 5 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx 1+{\sqrt[{3\,}]{\frac {442}{45}}}=3{,}14159125\ldots$   .

VI

Wie oben erhält man dann auch wegen

$\left(\pi -3\right)^{2}\approx 0{,}0200{\overline {48}}$   .

die auf 7 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx 3+{\sqrt {\frac {827}{41250}}}=3{,}141592672\ldots$   .

VII

Es ist

${\pi }^{15}=28658145{,}96938\ldots \approx 28658146=2\cdot 11\cdot 1103\cdot 1181$   .

Also ergibt sich die auf 9 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\sqrt[{15\,}]{28658146}}={\sqrt[{15\,}]{2\cdot 11\cdot 1103\cdot 1181}}$   .

VIII

Es ist

${\frac {1}{{\pi }^{3}-31}}=159{,}31988762105\ldots \approx 159{,}32={\frac {15932}{100}}={\frac {3983}{25}}$   .

Also ergibt sich die auf 9 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx {\sqrt[{3\,}]{31+{\frac {25}{3983}}}}={\sqrt[{3\,}]{\frac {123498}{3983}}}=3{,}1415926534402\ldots$   .

IX

Es ist

$\left({\sqrt {5}}\right)^{\pi }=5^{\frac {\pi }{2}}=12{,}52966660\ldots \approx 12{,}529{\overline {6}}={\frac {37589}{3000}}$   .

Also ergibt sich die auf 8 korrekte Nachkommastellen genaue Näherungsdarstellung

$\pi \approx 3{,}1415926594033\ldots {\frac {2\cdot \left(\ln {37589}-\ln {3000}\right)}{\ln {5}}}$   .

X

Es ist

${\frac {1}{\left({\sqrt {\pi }}-1\right)^{8}}}=7{,}8889582773195\ldots \approx 7{,}{\overline {8}}={\frac {71}{9}}$   .

Also ergibt sich die auf 5 korrekte Nachkommastellen genaue Näherungsdarstellung

${\sqrt {\pi }}\approx 1+{\sqrt[{8\,}]{\frac {9}{71}}}=1{,}77245\ldots$   .

Weitere Näherungen ähnlicher Art zu anderen Konstanten

I

Man findet in der gezeigten Art und Weise auch eine schöne Näherung für die Euler-Mascheroni-Konstante ${\gamma }$.

Es ist nämlich

${\frac {1}{{\gamma }^{2}}}=3{,}001399\ldots \approx 3{,}0014$   .

Damit ergibt sich die auf 7 korrekte Nachkommastellen genaue Näherungsdarstellung

$\gamma \approx {\sqrt {\frac {5000}{15007}}}$   .

II

Ebenso findet man auch eine Näherung für ${\sqrt {2}}$.

Es ist nämlich

$14\cdot {\sqrt {2}}=19{,}798989873\ldots \approx 19{,}7{\overline {98}}$   .

Damit ergibt sich die auf 8 korrekte Nachkommastellen genaue Näherungsdarstellung

${\sqrt {2}}\approx {\frac {19601}{13860}}=1+{\frac {5741}{13860}}$   .

Anmerkungen

• Die letzten Näherungsdarstellungen lassen sich noch verbessern; nämlich in dem Sinne, dass bei gleicher oder besserer Genauigkeit hinsichtlich der Anzahl der korrekten Nachkommastellen Brüche mit kleineren Nennern auftreten. Die - in einem spezifischen Sinne - besten Näherungen lassen sich nach einem Satz von Lagrange bekanntlich aus den Näherungsbrüchen der Kettenbruchentwicklungen gewinnen. Allerdings bedeutet es einen gewissen Aufwand, die Kettenbruchentwicklung einer Zahl zu erhalten, während man in den obigen Beispielen zu guten Näherungsdarstellungen allein durch Einsatz elementarer Methoden gelangt.
• Hier wäre auch auf eine (weniger bekannte) Arbeit von C. G. Specht aus dem Jahre 1828 hinzuweisen, mit der man eine auf 9 korrekte Nachkommastellen genaue Näherungsdarstellung der Kreiszahl gewinnt:

${\frac {7}{10^{7}}}+{\frac {13{\sqrt {146}}}{50}}=3{,}1415926531...$

Literatur

• Jörg Arndt, Christoph Haenel (Hrsg.): Pi. Algorithmen, Computer, Arithmetik. 2., überarbeitete und erweiterte Auflage. Springer, Berlin (u. a.) 2000, ISBN 3-540-66258-8, S. 57 ff. 
• S. Ramanujan: Modular equations and approximations to π. In: The Quarterly Journal of Mathematics. Band 45, 1914, S. 350–372.  MR2280849

Einzelnachweise und Fußnoten

rreferences />

Eine Determinantenidentität für den Sinus

Diese Identität ergibt sich unter Anwendung der Analysis als Folge der goniometrischen Additionstheoreme.

Sie gilt für beliebige $u,v,w\in \mathbb {C}$ und besagt:

${\begin{aligned}\Delta (u,v,w)&:={\begin{vmatrix}\sin {(v-w)}&-\sin {u}&\sin {u}\\\sin {v}&\sin {(w-u)}&-\sin {v}\\-\sin {w}&-\sin {w}&\sin {(u-v)}\\\end{vmatrix}}\\&=\sin {(u-v)}\cdot \sin {(v-w)}\cdot \sin {(w-u)}+\sin {u}\cdot \sin {v}\cdot \sin {(u-v)}+\sin {v}\cdot \sin {w}\cdot \sin {(v-w)}+\sin {w}\cdot \sin {u}\cdot \sin {(w-u)}\\&=0\\\end{aligned}}$

Literatur

• I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9, S. 157 ff. 

Einzelnachweise und Fußnoten

Kreferences />

Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie

Formulierung

Der Projektionssatz, welcher dem Kosinussatz zugrundeliegt (und mit diesem sogar gleichwertig ist), besagt:

Werden für ein Dreieck der euklidischen Ebene - wie üblich - mit $a,b,c>0$ die Längen der zugehörigen Seiten bezeichnet und mit $\alpha ,\beta ,\gamma \in \;]0,\pi [\;\;(\alpha +\beta +\gamma =\pi )$ die Innenwinkel dieses Dreiecks, gemessen im Bogenmaß, so gelten folgende Identitäten:

$a=b\cos {\gamma }+c\cos {\beta }$

$b=c\cos {\alpha }+a\cos {\gamma }$

$c=a\cos {\beta }+b\cos {\alpha }$

Aus dem Projektionssatz lässt sich nun die nachstehende Kosinusformel ableiten:

(F1) ${\cos }^{2}{\alpha }+{\cos }^{2}{\beta }+{\cos }^{2}{\gamma }+2\cos {\alpha }\cos {\beta }\cos {\gamma }=1$

Zusatz:

Aufgrund der Tatsache, dass die reelle Kosinusfunktion zu einer auf der ganzen komplexen Ebene erklärten holomorphen Funktion fortgesetzt werden kann, und wegen des Identitätssatzes gilt (F1) auch für alle komplexen Argumente $\alpha ,\beta ,\gamma \;\;{\text{mit }}\alpha +\beta +\gamma =\pi$   .

Darüber hinaus gelten stets die Ungleichungen

(U) $1\leq \max {{\bigl (}|\cos {\alpha }|+|\cos {\beta }|,|\cos {\beta }|+|\cos {\gamma }|,|\cos {\gamma }|+|\cos {\alpha }|{\bigr )}}$

und

(V) $1<|\cos {\alpha }|+|\cos {\beta }|+|\cos {\gamma }|$ .

Beweis

Herleitung der Ungleichung (F1)

Schreibt man die drei Gleichungen des Projektionssatzes in Matrizenform, so erhält man:

${\begin{pmatrix}-1&\cos {\gamma }&\cos {\beta }\\\cos {\gamma }&-1&\cos {\alpha }\\\cos {\beta }&\cos {\alpha }&-1\\\end{pmatrix}}\cdot {\begin{pmatrix}a\\b\\c\\\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\\end{pmatrix}}\in \mathbb {R} ^{3}$

Das bedeutet: Der Kern des zu der obigen Matrix gehörigen, auf dem $\mathbb {R} ^{3}$ definierten linearen Endomorphismus besteht nicht allein aus dem Nullvektor und ist daher kein Automorphismus.

Folglich muss die Determinante der Matrix gleich Null sein.

Unter Anwendung des laplaceschen Entwicklungssatzes und durch Entwicklung nach der ersten Zeile gewinnt man daraus:

${\begin{aligned}0&=(-1)\cdot {\begin{vmatrix}-1&\cos {\alpha }\\\cos {\alpha }&-1\\\end{vmatrix}}-\cos {\gamma }\cdot {\begin{vmatrix}\cos {\gamma }&\cos {\alpha }\\\cos {\beta }&-1\\\end{vmatrix}}+\cos {\beta }\cdot {\begin{vmatrix}\cos {\gamma }&-1\\\cos {\beta }&\cos {\alpha }\\\end{vmatrix}}\\&=(-1)\cdot {\bigl (}1-{\cos {\alpha }}^{2}{\bigr )}-\cos {\gamma }\cdot {\bigl (}-\cos {\gamma }-\cos {\alpha }\cos {\beta }{\bigr )}+\cos {\beta }\cdot {\bigl (}\cos {\alpha }\cos {\gamma }+\cos {\beta }{\bigr )}\\&=-1+{\cos }^{2}{\alpha }+{\cos }^{2}{\beta }+{\cos }^{2}{\gamma }+2\cos {\alpha }\cos {\beta }\cos {\gamma }\\\end{aligned}}$

Das beweist die Gültigkeit von (F1) .

Herleitung der Ungleichungen (U) und (V)

Zu (U)

Die erste Matrixgleichung oben lässt sich auch anders schreiben, nämlich wie folgt:

${\begin{pmatrix}0&\cos {\gamma }&\cos {\beta }\\\cos {\gamma }&0&\cos {\alpha }\\\cos {\beta }&\cos {\alpha }&0\\\end{pmatrix}}\cdot {\begin{pmatrix}a\\b\\c\\\end{pmatrix}}={\begin{pmatrix}a\\b\\c\\\end{pmatrix}}$

Das bedeutet: $1$ ist Eigenwert der links stehenden Matrix.

Die Ungleichung (U) ergibt sich dann unmittelbar durch Anwendung des Gerschgorin'schen Kreisesatzes !

Zu (V)

Um (V) zu zeigen, ist zunächst zu bemerken, dass (U) unmittelbar

$1\leq |\cos {\alpha }|+|\cos {\beta }|+|\cos {\gamma }|$

nach sich zieht. Also bleibt allein nachzuweisen, dass hier der Fall der Gleichheit auszuschließen ist.

Geht man hier jedoch im Gegenteil von der Gleichheit aus, so hat man – o.B.d.A. $|\cos {\alpha }|\geq |\cos {\beta }|\geq |\cos {\gamma }|$ annehmend – sogleich

$1=|\cos {\alpha }|+|\cos {\beta }|+|\cos {\gamma }|=|\cos {\alpha }|+|\cos {\beta }|$

und damit

$\cos {\gamma }=0$ .

Da wir jedoch ein nicht-ausgeartetes Dreieck zugrundelegen, hat man wegen $\gamma \in ]0,\pi [$ sofort

$\gamma ={\frac {\pi }{2}}$

und dann auch

$\alpha +\beta ={\frac {\pi }{2}}$ .

Also folgt

$1=|\cos {\alpha }|+|\cos {({\frac {\pi }{2}}-\alpha )}|$

und dann sogleich

$1=|\cos {\alpha }|+|\sin {\alpha }|$

und weiter

${\cos ^{2}}{\alpha }+{\sin ^{2}}{\alpha }=1={\cos ^{2}}{\alpha }+2|\cos {\alpha }\sin {\alpha }|+{\sin ^{2}}{\alpha }$ .

Dann muss aber

$2\cos {\alpha }\sin {\alpha }=0$

gelten und infolge der Additionstheoreme weiter

$\sin {2\alpha }=0$ .

Wegen $\alpha \in ]0,\pi [$ ist $2\alpha \in ]0,2\pi [$ und es folgt

$2\alpha =\pi$

und damit

$\alpha ={\frac {\pi }{2}}$ .

Dann muss aber auch

$\beta =0$

sein, was aber mit der Tatsache unvereinbar ist, dass auch $\beta \in ]0,\pi [$ vorausgesetzt ist.

Damit ist ein Widerspruch gegeben, was bedeutet, dass die obige Annahme der Gleichheit nicht haltbar ist.

Anwendungen

A-1

Aus (F1) lassen sich leicht weitere (mehr oder weniger bekannte) Formeln ableiten.

A-1-1

Behält man in (F1) $\alpha$ als Variable und setzt dann $\beta ={\frac {\pi }{2}}-\alpha \;,\;\gamma ={\frac {\pi }{2}}$   , so erhält man wegen ${\cos }({\frac {\pi }{2}})=0$ direkt

${\cos }^{2}{\alpha }+{\cos }^{2}({\frac {\pi }{2}}-\alpha )+0+0=1$

und damit die bekannte Identität

${\cos }^{2}{\alpha }+{\sin }^{2}(\alpha )=1$   .

A-1-2

Mit A-1-1 folgert man dann direkt weiter:

(F1') ${\sin }^{2}{\alpha }+{\sin }^{2}{\beta }+{\sin }^{2}{\gamma }-2\cos {\alpha }\cos {\beta }\cos {\gamma }=2$ für $\alpha ,\beta ,\gamma \in \mathbb {C} \;\;{\text{mit }}\alpha +\beta +\gamma =\pi$   .

A-2

Hat man $\alpha ,\beta ,\gamma \in ]0,{\frac {\pi }{2}}]\mathrm {\text{ mit }} \gamma =\pi -\alpha -\beta$, so erhält man aus in (F1) , indem man mittels quadratischer Ergänzung nach $\cos {\gamma }$ auflöst, die folgende Gleichung:

(F2) $\cos {\gamma }=\cos {\alpha }\cdot \cos {\beta }+{\sqrt {1+{\cos }^{2}{\alpha }\cdot {\cos }^{2}{\beta }-{\cos }^{2}{\alpha }-{\cos }^{2}{\beta }}}$   .

Durch Anwendung von (F2) gewinnt man aus bekannten Kosinuswerten leicht neue, und zwar insbesondere solche, in denen allein natürliche Zahlen, Brüche und Wurzeln auftreten.

Beispiele dafür sind die folgenden.

A-2-1

Man setzt in (F2) $\alpha ={\frac {\pi }{3}}\;,\;\beta ={\frac {\pi }{4}}\;,\;\gamma ={\frac {5\pi }{12}}$ und erhält

$\cos {\frac {5\pi }{12}}=-{\frac {1}{2}}\cdot {\frac {\sqrt {2}}{2}}+{\sqrt {1+{\frac {1}{4}}\cdot {\frac {2}{4}}-{\frac {1}{4}}-{\frac {2}{4}}}}={\frac {-{\sqrt {2}}+{\sqrt {16+2-4-8}}}{4}}$   .

Also ist

$\cos {\frac {5\pi }{12}}={\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$   .

A-2-2

Man setzt in (F2) $\alpha ={\frac {\pi }{2}}\;,\;\beta ={\frac {5\pi }{12}}\;,\;\gamma ={\frac {\pi }{12}}$ und erhält

$\cos {\frac {\pi }{12}}=0+{\sqrt {1+0+0-{\cos }^{2}({\frac {5\pi }{12}})}}={\sqrt {1-{\bigl (}{\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}{\bigr )}^{2}}}$   .

Also ist

$\cos {\frac {\pi }{12}}={\frac {\sqrt {8+4\cdot {\sqrt {3}}}}{4}}$

und damit

$\cos {\frac {\pi }{12}}={\frac {\sqrt {2+{\sqrt {3}}}}{2}}$

oder auch

$\cos {\frac {\pi }{12}}={\frac {{\sqrt {3}}+1}{2{\sqrt {2}}}}$   .

Quellen und Hintergrundliteratur

• Hans-Jochen Bartsch: Taschenbuch mathematischer Formeln. 18., verbesserte Auflage. Fachbuchverlag Leipzig im Carl Hanser Verlag]], München, Wien 1998, ISBN 3-446-19396-0, S. 173. 
• Heinrich Behnke, Friedrich Bachmann, Kuno Fladt, Wilhelm Süss (Hrsg.): Grundzüge der Mathematik. Band II. Geometrie. Vandenhoeck & Ruprecht, Göttingen 1960, S. 226 ff. 
• I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9, S. 76–83, 145–146. 
• George S. Carr: Formulas and Theorems in Pure Mathematics. Früher: A Synopsis of Elementary Results in Pure Mathematics, London & Cambridge 1886. 2. Auflage. Chelsea Publishing Company, New York 1970, S. 159–171. 
• Hanfried Lenz: Grundlagen der Elementarmathematik. 3., überarbeitete Auflage. Hanser Verlag, München (u. a.) 1976, ISBN 3-446-12160-9, S. 236. 

Einzelnachweise und Fußnoten

rreferences />

Neue (?) Identitäten für Sinus und Kosinus

Es werden im Rahmen der Trigonometrie zwei Identitäten für Sinus und Kosinus hergeleitet.

Formulierung

Für $u,v,w\in \mathbb {C} \mathrm {\text{ mit }} u+v+w=\pi$ gelten:

(1) $\sin(-u+v+w)+\sin(u-v+w)+\sin(u+v-w)=\sin(2u)+\sin(2v)+\sin(2w)$

(2) $\cos(-u+v+w)+\cos(u-v+w)+\cos(u+v-w)=(-1)\cdot {\bigl (}\cos(2u)+\cos(2v)+\cos(2w){\bigr )}$

Für $u,v\in \mathbb {C}$ gelten:

(3) ${\bigl (}\sin u+\sin v-\sin(u+v){\bigr )}\cdot {\bigl (}1+\cos u+\cos v+\cos(u+v){\bigr )}=2\cdot \sin u\cdot \sin v\cdot \sin(u+v)$

(4) ${\bigl (}1-\cos u{\bigr )}\cdot {\bigl (}1+\sin u+\cos u{\bigr )}\cdot {\bigl (}1+\cos u-\sin u{\bigr )}=\sin u\cdot \sin(2u)$

Beweis

Seien $u,v,w\in \mathbb {C} \mathrm {\text{ und dabei }} u+v+w=\pi$.

Dann gilt:

Ad (1):

${\begin{aligned}\sin(2u)&=-\sin(-2u)\\&=\sin(-2u+\pi )\\&=\sin(-2u+u+v+w)\\&=\sin(-u+v+w)\\\end{aligned}}$

Ad (2):

${\begin{aligned}-\cos(2u)&=-\cos(-2u)\\&=\cos(-2u+\pi )\\&=\cos(-2u+u+v+w)\\&=\cos(-u+v+w)\\\end{aligned}}$

Quellen und Hintergrundliteratur

• I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9, S. 80–83. 
• Konrad Knopp: Theorie und Anwendung der unendlichen Reihen (= Die Grundlehren der Mathematischen Wissenschaften. Band 2). 5., berichtigte Auflage. Springer Verlag, Berlin/ Göttingen/ Heidelberg/ New York 1964, ISBN 3-540-03138-3.  MR0183997

Satz von der Mittelparallelen im Dreieck

Der Satz von der Mittelparallelen im Dreieck ist ein Lehrsatz aus dem mathematischen Teilgebiet der Dreiecksgeometrie. Der Satz behandelt eine elementare Eigenschaft der Dreiecke der euklidischen Ebene.

Formulierung des Satzes

Der Satz besagt folgendes:

In einem Dreieck der euklidischen Ebene ist die Verbindungsstrecke der Mittelpunkte zweier Seiten stets parallel zur dritten Dreiecksseite und stets halb so lang wie diese.

Beweis

Der Satz ergibt sich elementargeometrisch, wobei die Parallelitätsbehauptung aus der Umkehrung des ersten Strahlensatzes folgt, während die Aussage über das Längenverhältnis sich dann mit dem zweiten Strahlensatz ergibt.

Ein anderer Beweis unter Verwendung der Vektorrechnung geht wie folgt:

Ausgehend von der Festlegung (vgl. Bild), dass das Dreieck die Eckpunkte $A,B,C$ hat und dass $D$ der Mittelpunkt der Seite $[AB]$ ist und $E$ der Mittelpunkt der Seite $[AC]$, setzt man

${\vec {a}}={\overrightarrow {BC}}\;,\;{\vec {b}}={\overrightarrow {CA}}\;,\;{\vec {c}}={\overrightarrow {AB}}\;,\;{\vec {m}}_{a}={\overrightarrow {DE}}$   .

Man erhält daraus die Gleichungen

${\frac {1}{2}}{\vec {b}}={\overrightarrow {CE}}={\overrightarrow {EA}}\;,\;{\frac {1}{2}}{\vec {c}}={\overrightarrow {AD}}={\overrightarrow {DB}}$   .

Damit folgt

${\vec {m}}_{a}+{\frac {1}{2}}{\vec {b}}+{\frac {1}{2}}{\vec {c}}={\vec {0}}$

sowie

${\vec {m}}_{a}-{\frac {1}{2}}{\vec {b}}-{\vec {a}}-{\frac {1}{2}}{\vec {c}}={\vec {0}}$   .

Durch Addieren der linken und der rechten Seiten der letzten beiden Gleichungen erhält man dann

$2{\vec {m}}_{a}-{\vec {a}}={\vec {0}}$

und damit

${\vec {m}}_{a}={\frac {1}{2}}{\vec {a}}$   .

Daraus ergibt sich einerseits, dass die beiden Geraden, auf denen die Strecken $[BC]$ bzw. $[DE]$ liegen, in derselben Richtung verlaufen und damit parallel sind, und andererseits, dass die Längen der beiden Strecken $[BC]$ und $[DE]$ die behauptete Beziehung , nämlich

${\overline {DE}}={\frac {1}{2}}{\overline {BC}}$

erfüllen.

Für die beiden anderen Mittelparallelen geht der Beweis entsprechend.

Quellen und Literatur

• I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9. 
• Siegfried Krauter: Erlebnis Elementargeometrie. Ein Arbeitsbuch zum selbstständigen und aktiven Entdecken. Spektrum Akademischer Verlag, München 2005, ISBN 3-8274-1644-2. 
• Wilhelm Kuypers, Josef Lauter (Hrsg.): Mathematik Sekundarstufe II. Analytische Geometrie und Lineare Algebra. Cornelsen Verlag, 1992. 

Einzelnachweise und Fußnoten

Kreferences />

KKKategorie:Satz (Mathematik)|Mittelparallelen im Dreieck, Satz von der]] KKKategorie:Dreiecksgeometrie]]

Kosinussatz (Ergänzungen)

Der Kosinussatz ist ein elementarer Lehrsatz der Trigonometrie, einem der Teilgebiete der Mathematik. Er beinhaltet drei Identitätsgleichungen, welche die Beziehungen zwischen den Längen der Seiten von Dreiecken und den Kosinuswerten ihrer Winkel darstellen.

Formulierung

Allgemeine Formulierung

Bezeichnungen im Dreieck

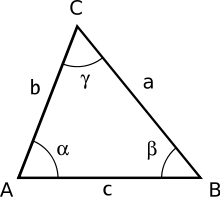
Für die drei Seiten $a$, $b$ und $c$ eines Dreiecks sowie für den der Seite $c$ gegenüberliegenden Winkel (d. h. den zwischen den Seiten $a$ und $b$ liegenden Winkel) $\gamma$ gilt:

$c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma$

Entsprechend gilt für die anderen Winkel:

$b^{2}=a^{2}+c^{2}-2\,a\,c\,\cos \beta$

$a^{2}=b^{2}+c^{2}-2\,b\,c\,\cos \alpha$

Gleichwertige Formulierung

Die zuvor genannten drei Identitätsgleichungen sind ihrerseits Folgerungen aus (und im Rahmen der Trigonometrie der euklidischen Ebene sogar gleichwertig mit) den folgenden drei Kosinusformeln:

$a=b\cos {\gamma }+c\cos {\beta }$

$b=c\cos {\alpha }+a\cos {\gamma }$

$c=a\cos {\beta }+b\cos {\alpha }$

Man fasst diese Formeln unter dem Stichwort Projektionssatz oder Projektionssätze zusammen.

Beweis

Elementargeometrischer Beweis

....

Beweis mittels Vektorrechnung

Anschließend an die Darstellung von Gericke und Raith wird zunächst der Beweis der obigen drei Kosinusformeln (s. Abschnitt „Gleichwertige Formulierung“) geführt:

Dazu macht man man die Festlegungen

${\vec {a}}={\overrightarrow {BC}}\;,\;{\vec {b}}={\overrightarrow {CA}}\;,\;{\vec {c}}={\overrightarrow {AB}}$  .

Man erhält daraus die Gleichungen

$-{\vec {a}}={\overrightarrow {CB}}\;,\;-{\vec {b}}={\overrightarrow {AC}}\;,\;-{\vec {c}}={\overrightarrow {BA}}$

sowie unter Benutzung der Eigenschaften des Skalarprodukts

$a=|{\vec {a}}|=|-{\vec {a}}|\;,\;b=|{\vec {b}}|=|-{\vec {b}}|\;,\;c=|{\vec {c}}|=|-{\vec {c}}|$

und

$\cos {\alpha }={\frac {\langle -{\vec {b}},{\vec {c}}\rangle }{|-{\vec {b}}|\cdot |{\vec {c}}|}}={\frac {\langle -{\vec {b}},{\vec {c}}\rangle }{bc}}\;,\;\cos {\beta }={\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{|-{\vec {c}}|\cdot |{\vec {a}}|}}={\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{ca}}\;,\;\cos {\gamma }={\frac {\langle -{\vec {a}},{\vec {b}}\rangle }{|-{\vec {a}}|\cdot |{\vec {b}}|}}={\frac {\langle -{\vec {a}},{\vec {b}}\rangle }{ab}}$   .

Nun zieht man die für das Dreieck charakteristische Grundgleichung

${\vec {a}}+{\vec {b}}+{\vec {c}}={\vec {0}}$

heran und gewinnt

${\vec {a}}=(-{\vec {b}})+(-{\vec {c}})$

und weiter

$a^{2}=|{\vec {a}}|^{2}=\langle {\vec {a}},{\vec {a}}\rangle =\langle -{\vec {b}},{\vec {a}}\rangle +\langle -{\vec {c}},{\vec {a}}\rangle$   .

Folglich ergibt sich

$a={\frac {\langle -{\vec {b}},{\vec {a}}\rangle }{a}}+{\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{a}}={\frac {\langle -{\vec {a}},{\vec {b}}\rangle }{a}}+{\frac {\langle -{\vec {c}},{\vec {a}}\rangle }{a}}=b\cos {\gamma }+c\cos {\beta }$

und damit die erste der obigen drei Kosinusformeln.

Die beiden anderen erhält man auf gleiche Art und Weise.

Auf die drei Formeln der allgemeinen Formulierung kann man dann mittels elementarer algebraischer Operationen schließen. So erhält man (etwa) die erste Gleichung, indem die in den zuvor stehenden drei Kosinusformeln nacheinander mit $a\;,\;b\;,\;(-c)$ multipliziert, aufaddiert und nach $c^{2}$ auflöst.

Quellen und Literatur

• Heinrich Behnke, Friedrich Bachmann, Kuno Fladt, Wilhelm Süss (Hrsg.): Grundzüge der Mathematik. Band II. Geometrie. Vandenhoeck & Ruprecht, Göttingen 1960, S. 226–277. 
• I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9. 
• Hanfried Lenz: Grundlagen der Elementarmathematik. 3., überarbeitete Auflage. Hanser Verlag, München (u. a.) 1976, ISBN 3-446-12160-9. 

Weblinks

KKCommonscat|Law of cosines}}

• Kosinussatz – Illustration und Beweis auf www.arndt-bruenner.de
• Herleitung des Kosinussatzes sowie Anwendung (Video)
• Law of Cosines – 2 Beweise auf proofwiki.org (englisch)

Einzelnachweise und Fußnoten

Kreferences />

KKKategorie:Trigonometrie]] KKKategorie:Satz (Mathematik)]]

Kennzeichnung der rechtwinkligen Dreiecke der euklidischen Ebene (Unfertig)

Bekanntlich liefert der Satz des Pythagoras eine Charakterisierung der rechtwinkligen Dreiecke der euklidischen Ebene. Diese Charakterisierung geschieht in der Weise, dass anstelle der Rechtwinkligkeitsbedingung das Erfülltsein der pythagoreischen Gleichung tritt. In gleicher Weise lassen sich viele andere charakteristische Gleichungen finden, welche anstelle der pythagoreischen Gleichung treten. Eine davon ist die folgende, welche Höhen- und Seitenlängen in Beziehung bringt.

Formulierung

Gegeben sei ein Dreieck   $\triangle ABC$   der euklidischen Ebene mit   $a=|BC|$   ,   $b=|AC|$   sowie   $c=|AB|$   und dabei sei   $\triangle ABC$   ohne stumpfe Winkel.

Für den Höhenfußpunkt   $F\in AB$   gegenüber von   $C$   sei   $h=|CF|$   die Höhenlänge.

Weiter seien   $p=|AF|$   und   $q=|BF|$   , also   $c=p+q$   , sowie   $\gamma$   der Innenwinkel beim Punkte   $C$   (gemessen in Altgrad), welcher zugleich der größte der drei Innenwinkel sei.

Dann gilt:

$\gamma =90^{\circ }$   $\iff$   ${\frac {1}{h^{2}}}={\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}$   .

Beweis

=>

Die zu zeigende Gleichung ist gleichwertig mit

$h^{2}={\frac {1}{{\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}}}$   ,

also gleichwertig mit

$h^{2}={\frac {a^{2}b^{2}}{a^{2}+b^{2}}}$

und dann mit

$h^{2}(a^{2}+b^{2})=a^{2}b^{2}$   .

Da   $\gamma =90^{\circ }$   vorausgesetzt wird, ist dies nach Pythagoras gleichbedeutend mit

$h^{2}c^{2}=a^{2}b^{2}$

und damit auch mit

$hc=ab$

und schließlich mit

${\frac {hc}{2}}={\frac {ab}{2}}$   .

Letztere Gleichung aber gilt nach der Dreiecksflächenformel.

q.e.d

<=

Nach Pythagoras gilt (bezogen auf die Teildreiecke) wiederum

$p^{2}=b^{2}-h^{2}$

und

$q^{2}=a^{2}-h^{2}$   .

Also folgt aus ${\frac {1}{h^{2}}}={\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}$

zunächst wie oben

$h^{2}={\frac {a^{2}b^{2}}{a^{2}+b^{2}}}$   .

Damit hat man weiter

$p^{2}={\frac {b^{2}(a^{2}+b^{2})-a^{2}b^{2}}{a^{2}+b^{2}}}={\frac {b^{4}}{a^{2}+b^{2}}}$

und ganz entsprechend

$q^{2}={\frac {a^{4}}{a^{2}+b^{2}}}$   .

Das ergibt

$pq={\frac {a^{2}b^{2}}{a^{2}+b^{2}}}$   .

und damit

${\begin{aligned}c^{2}&=(p+q)^{2}\\&=p^{2}+2pq+q^{2}\\&={\frac {b^{4}}{a^{2}+b^{2}}}+{\frac {2a^{2}b^{2}}{a^{2}+b^{2}}}+{\frac {a^{4}}{a^{2}+b^{2}}}\\&={\frac {(a^{2}+b^{2})^{2}}{a^{2}+b^{2}}}\\&=a^{2}+b^{2}\\\end{aligned}}$   .

Nun ist nach dem Kosinussatz

$c^{2}=a^{2}+b^{2}-2ab{\cos \gamma }$   .

Folglich ist

$\cos \gamma =0$  

und daher unter Berücksichtigung von   $0^{\circ }\leq \gamma \leq 180{^{\circ }}$  

wie gewünscht $\gamma =90^{\circ }$   .

q.e.d

Literatur

• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 2. 13. Auflage. Ernst Klett Verlag, Stuttgart 1965. 
• H. Fenkner, K. Holzmüller: Mathematisches Unterrichtswerk. Nach den Richtlinien für die Lehrpläne der höheren Schulen Preußens neu bearbeitet von Dr. Karl Holzmüller. Geometrie. Ausgabe A in 2 Teilen. I. Teil. 12. Auflage. Verlag von Otto Salle, Berlin 1926. 
• A. M. Fraedrich: Die Satzgruppe des Pythagoras (= Lehrbücher und Monographien zur Didaktik der Mathematik. Band 29). B.I.-Wissenschaftsverlag, Mannheim - Leipzig - Wien - Zürich 1994, ISBN 3-411-17321-1. 

WEITERES ZUR LYM-UNGLEICHUNG

Spätestens seit Lubells einfacher Herleitung des Satzes von Sperner mit Hilfe der LYM-Ungleichung nimmt diese in der Spernertheorie einen zentralen Platz ein. Nach Lubells Artikel wurde eine Fülle von Ergebnissen über den Zusammenhang zwischen der LYM-Ungleichung bzw. LYM-artigen Ungleichungen und der Spernertheorie vorgelegt.

Die Ahlswede-Zhang-Identität

Diese Identität (auch AZ-Identität genannt, in der englischsprachigen Literatur als AZ identity bezeichnet ) geht auf die beiden Mathematiker Rudolf Ahlswede und Zhen Zhang zurück. Sie stellt eine Verschärfung der LYM-Ungleichung dar und lässt sich formulieren wie folgt:

Gegeben sei eine endliche Menge   $M$   mit   $n$   Elementen (   $n\in \mathbb {N}$   ) und dazu ein nicht-leeres Mengensystem   ${\mathcal {A}}\neq \emptyset$   von nicht-leeren Teilmengen von $M$, also eine nicht-leere Teilmenge der reduzierten Potenzmenge ${\mathcal {P}}(M)\setminus \{\emptyset \}$   .

Weiter sei für   $X\subseteq M$   :

$D_{\mathcal {A}}(X)={\begin{cases}\ \;\,\bigcap \{A\mid A\in {\mathcal {A}}\land A\subseteq X\}&\exists A\in {\mathcal {A}}:A\subseteq X\\\ \;\,\emptyset &\mathrm {sonst} \end{cases}}$

Dann gilt:

$\sum _{\emptyset \neq X\subseteq M}{\frac {|D_{\mathcal {A}}(X)|}{|X|\cdot {\binom {n}{|X|}}}}=1$

Ist   ${\mathcal {A}}$   eine Antikette von ${\mathcal {P}}(X)$ und   $A\in {\mathcal {A}}$   , so ist   $D_{\mathcal {A}}(A)=A$ . Also ist   $\sum _{A\in {\mathcal {A}}}{\frac {1}{\binom {n}{|A|}}}=\sum _{A\in {\mathcal {A}}}{\frac {|A|}{|A|\cdot {\binom {n}{|A|}}}}$   in der obigen Summe enthalten, was was zeigt, dass die AZ-Identität die LYM-Ungleichung unmittelbar impliziert.

Zusammenhang mit Gruppenoperationen

In der Kombinatorik besteht einer der klassischen Ansätze, den berühmten Satz von Sperner (1928) zu beweisen darin, zunächst die Lubell-Yamamoto-Meshalkin-Ungleichung - kurz LYM-Ungleichung genannt - zu zeigen und daraus dann den spernerschen Satz zu folgern.

Hierbei gelangt man zu der einfachen, jedoch wichtigen Beobachtung, dass bei einer endlichen Potenzmenge   $2^{M}$   über einer endlichen Grundmenge   $M$   die Automorphismengruppe   $\operatorname {Aut} (2^{M})$   mit der symmetrischen Gruppe   $S_{M}$ über $M$   identifiziert werden kann:

Denn jeder solcher Automorphismus zeichnet sich dadurch aus, dass er die Inklusionsordnung der Potenzmenge strikt erhält, weswegen er stets mit einer Permutation der Atome des booleschen Verbandes   $2^{M}$   - also der einelementigen Teilmengen von   $M$   ! - zusammengehört, welche ihn wegen der Verbandseigenschaften von   $2^{M}$   völlig bestimmt.

Daher ist jeder der zugehörigen Orbits

$\operatorname {Aut} (2^{M})\cdot X=S_{M}\cdot X=\{g(X):g\in S_{M}\}\;(X\subseteq M)$

nichts weiter sind als eine der Mächtigkeitsklassen

${M \choose i}\subseteq 2^{M}\;(i=0,\ldots ,|M|)$  ,

da nämlich für   $X\subseteq M$   die Menge   $g(X)$   nichts anderes ist als die Menge der   $g$-Bilder von   $X$   unter der Permutation $g$.

Geht man nun von   $\operatorname {Aut} (2^{M})$   zu beliebigen endlichen Gruppen und allgemeinen Gruppenoperationen über, so erhält man eine Verallgemeinerung der LYM-Ungleichung, welche sogar ganz unabhängig von den Ordnungsbetrachtungen innerhalb der endlichen Potenzmengen Gültigkeit hat.

Formulierung der Verallgemeinerung

Gegeben sei eine endliche (multiplikativ geschriebene) Gruppe $(G,\cdot )$ mit neutralem Element $e$.

$S$ sei eine endliche Menge und hierauf operiere $(G,\cdot )$ vermöge der Gruppenoperation

$G\times S\to S$

$(g,s)\mapsto g\cdot s$.

Weiter seien eine Teilmenge $A\subseteq S$ gegeben und eine endliche Familie $(c_{i})_{i\in I}$ von Elementen von $S$, wobei $I$ eine endliche nichtleere Indexmenge sein möge.

Dabei sei für $g\in G$

$I_{g}=\{i\in I:{g\cdot c_{i}}\in A\}$   .

Dann gilt  :

$\sum _{i\in I}{\frac {|{G\cdot c_{i}}\cap {A}|}{|{G\cdot c_{i}}|}}\cdot w_{i}\leq \max _{g\in G}{\sum _{i\in I_{g}}{w_{i}}}$.

Beweis

Schritt 1

Wir setzen

$G^{i}=\{g\in G:{g\cdot c_{i}}\in A\}$   $(\forall i\in I)$   .

Damit gilt:

(1) $\bigcup _{i\in I}{G^{i}\times \{i\}}=\bigcup _{g\in G}{\{g\}\times I_{g}}$

Wenden wir, ausgehend von einer gegebenen Zahlenfamilie $(w_{i})_{i\in I}$, die reellwertige Funktion

$v\colon G\times I\to \mathbb {R} \;,\;v(g,i)=w_{i}$

auf (1) an, so erhalten wir aus Disjunktheitsgründen zunächst

(2) $\sum _{i\in I}{v(G^{i}\times \{i\})}=\sum _{g\in G}{v(\{g\}\times I_{g})}$

und daraus unmittelbar die Ungleichung

(3) $\sum _{i\in I}{v(G^{i}\times \{i\})}\leq |G|\max _{g\in G}{\;v(\{g\}\times I_{g})}$   .

Aus (3) gelangt man sogleich zu der Ungleichung

(4) $\sum _{i\in I}{|G^{i}|\cdot w_{i}}\leq |G|\max _{g\in G}{\;\sum _{i\in I_{g}}{w_{i}}}$   .

Mit (4) jedoch ergibt sich sofort die Behauptung, wenn noch für jeden Index $i\in I$ die folgende Identität (5) gezeigt wird:

(5) $|G^{i}|={\frac {|G|\cdot |{G\cdot c_{i}}\cap {A}|}{|{G\cdot c_{i}}|}}$   .

Schritt 2

Zum Beweis von (5) sei $j$ irgendeiner der Indizes. Der Vereinfachung halber sei $c:=c_{j}$ gesetzt.

Es ist dann

(6) $|G^{j}|=\sum _{a\in A}{|\{g\in G\colon g\cdot c=a\}|}=\sum _{a\in (G\cdot c\;\cap \;A)}{|\{g\in G\colon g\cdot c=a\}|}$   .

Nun lässt sich zu jedem $a\in (G\cdot c\;\cap \;A)$ ein Gruppenelement $h\in G$ als fest vorgegeben annehmen, welches die Gleichung $h\cdot c=a$ erfüllt .

Damit lässt sich beweisen - siehe Schritt 3 unten! - dass die Gleichung

(7) $hG_{c}=\{g\in G\colon g\cdot c=a\}$

besteht.

Und dies reicht aus zum Beweis von (5):

Denn man berücksichtigt erst einmal die Tatsache, dass jede Translation eine Bijektion ist, weswegen man mit (7) zunächst

(8) $|G^{j}|=|G_{c}||G\cdot c\;\cap \;A|$

hat. Dann wird weiter berücksichtigt, dass in die bisherigen Überlegungen keine speziellen Eigenschaften der Teilmenge $A\subseteq S$ eingeflossen sind, dass also (8) für jedes $A\subseteq S$ und dann inbesondere auch für $A=S$ richtig ist. Also folgt sogleich

(9) $|G|=|G_{c}||G\cdot c|$   .

Verknüpft man nun (8) und (9), so hat man (5).

Schritt 3

Zum Nachweis von (7) sind die Inklusion von links nach rechts und umgekehrt die Inklusion von rechts nach links zu zeigen.

Zunächst wird erstere gezeigt. Dazu sei $g^{'}\in G_{c}$.

Es gilt dann

(10) $(hg^{'})\cdot c=h\cdot (g^{'}\cdot c)=h\cdot c=a$

und folglich

(11) $hG_{c}\subseteq \{g\in G\colon g\cdot c=a\}$   .

Zum Nachweis der umgekehrten Inklusion sei $g\in G$ und dafür die Gleichung $g\cdot c=a$ erfüllt.

Dann ist wie stets

(12) $g=h(h^{-1}g)$

und hierbei gilt

(13) $(h^{-1}g)\cdot c=h^{-1}\cdot (g\cdot c)=h^{-1}\cdot a=h^{-1}\cdot (h\cdot c)=(h^{-1}h)\cdot c=e\cdot c=c$ .

Also haben wir

(14) $\{g\in G\colon g\cdot c=a\}\subseteq hG_{c}$   .

(11) und (14) zusammen ergeben (7) .

Korollar

Ist unter den oben beschriebenen Gegebenheiten die Sitution derart, dass jede der Indexmengen   $I_{g}\;(g\in G)$   aus höchstens einem einzigen Index besteht, so gilt insbesondere:

$\sum _{i\in I}{\frac {|{G\cdot c_{i}}\cap {A}|}{|{G\cdot c_{i}}|}}\cdot w_{i}\leq \max _{i\in I}\;{w_{i}}$.

Herleitung der LYM-Ungleichung

Diese verallgemeinerte LYM-Ungleichung umfasst die ursprüngliche Lubell-Yamamoto-Meshalkin-Ungleichung und andere verwandte Ungleichungen.

Um dies im Falle der LYM-Ungleichung einzusehen, betrachte man die oben schon erwähnte endliche Menge   $M$   und es sei ohne Beschränkung der Allgemeinheit angenommen, dass   $M=\{1,\ldots ,n\}$   für   $n\in \mathbb {N}$   gelte.

Man wendet die verallgemeinerte LYM-Ungleichung an für den Fall, dass

$S=2^{M}$

und

$G=\operatorname {Aut} (2^{M})=S_{M}$

und dann noch

$I=\{0,1,\ldots ,n\}$

ist .

Hierbei wird, wie oben dargelegt, die Automorphismengruppe $\operatorname {Aut} (2^{M})$ mit der symmetrischen Gruppe $S_{M}$ identifiziert.

Wie oben erwähnt, hat man als Operation

$S_{M}\times 2^{M}\to 2^{M}$

dabei

$(g,X)\mapsto {g\cdot X}=g(X)\;(g\in S_{M}\;,\;x\subseteq M)$

vorliegen.

Man legt nun für das obige   $A$   eine Antikette der Potenzmenge   $2^{M}$   zugrunde, also ein Mengensystem   ${\mathcal {A}}$   von Teilmengen von $M$, welches so beschaffen ist, dass von diesen Teilmengen keine zwei verschiedene einander umfassen.

Bedeutsam ist nun, dass man stets folgende Kette von Teilmengen innerhalb   $S=2^{M}$   hat:

$C_{0}=\emptyset$

sowie für   $i=1,\ldots ,n$

$C_{i}=\{1,\ldots ,i\}$   .

Damit hat man für   $i=0,\ldots ,n$:

$|S_{M}\cdot C_{i}|=|{M \choose i}|={n \choose i}$

und zudem

$S_{M}\cdot C_{i}\cap {\mathcal {A}}={M \choose i}\cap {\mathcal {A}}=\{X\in {\mathcal {A}}\colon |X|=i\}$   .

Weiter von Bedeutung ist die Klärung der Frage, wie groß für eine Permutation   $g$   das ihr zugehörige   $I_{g}$   sein kann. Dies ist jedoch unmittelbar einsichtig:

Denn da   ${\mathcal {A}}$   Antikette ist, kann es niemals vorkommen, dass für zwei unterschiedliche   $i,j$   - etwa   $i<j$   -   $g(C_{i}),g(C_{j})\in {\mathcal {A}}$   gilt, weil nämlich die Inklusion   $C_{i}\subset C_{j}$   stets die Inklusion   $g(C_{i})\subset g(C_{j})$   nach sich zieht (und umgekehrt).

Das heißt jedoch, dass für   $g\in S_{M}$   durchgängig

$|I_{g}|\leq 1$

gilt!

Bezeichnet man nun noch für   $i=0,\ldots ,n$   mit   ${a_{i}}$   die Anzahl der in   ${\mathcal {A}}$   vorkommenden Mengen, welche aus exakt   $i$   Elementen bestehen, so hat man:

$a_{i}=|S_{M}\cdot C_{i}\cap {\mathcal {A}}|$   .

Legt man dann noch die konstante Zahlenfamilie

$w_{0}=w_{1}=\ldots =w_{n}=1$  

zugrunde, so folgt aus dem Korollar unmittelbar die LYM-Ungleichung.

Quellen und Hintergrundliteratur

• Ian Anderson: Combinatorics of Finite Sets. Clarendon Press, Oxford 1987, ISBN 0-19-853367-5.  MR0892525
• Konrad Engel: Sperner Theory (= Encyclopedia of Mathematics and its Applications. Band 65). Cambridge University Press, Cambridge (u. a.) 1997, ISBN 0-521-45206-6.  MR1429390
• D. Lubell: A short proof of Sperner's lemma. Journal of Combinatorial Theory, Vol. 1, 2 (1966): 299. doi:10.1016/S0021-9800(66)80035-2, MR0194348
• L.D. Meshalkin: Generalization of Sperner's theorem on the number of subsets of a finite set. Theory of Probability and its Applications, Vol. 8, 2 (1963): 203–204. doi:10.1137/1108023, MR0150049
• Kurt Meyberg: Algebra. Teil 1 (= Mathematische Grundlagen für Mathematiker, Physiker und Ingenieure). Carl Hanser Verlag, München, Wien 1975, ISBN 3-446-11965-5.  [1]
• Hans-Josef Scholz: Über die Kombinatorik der endlichen Potenzmengen im Zusammenhang mit dem Satz von Sperner. Dissertation, Universität Düsseldorf (1987).
• Emanuel Sperner: Ein Satz über Untermengen einer endlichen Menge. Math. Z. 27 (1928): 544–548. MR1544925
• Koichi Yamamoto: Logarithmic order of free distributive lattice. Journal of the Mathematical Society of Japan, Vol. 6 (1954): 343–353. MR0067086.

Einzelnachweise und Fußnoten

KKreferences />

Weitere Anwendung: Ein allgemeiner Charakterisierungssatz zur LYM-Eigenschaft

Die oben dargestellte Verallgemeinerung der LYM-Ungleichung kann verstanden werden als ein Teilschritt hin zu einer allgemeinen Charakterisierung zur LYM-Eigenschaft (engl. LYM property), welche diese in Zusammenhang bringt mit dem Konzept der Operation von Gruppen auf Mengen..

Hierbei betrachtet man eine endliche teilweise geordnete Menge

$P\neq \emptyset$

mit der Ordnungsrelation

$\leq$ .

Dabei sei

${\mathcal {O}}=\{O_{1},\dots ,O_{t}\}\subseteq 2^{P}\;(|{\mathcal {O}}|=t\in \mathbb {N} )$

die Menge der verschiedenen Orbits

$\operatorname {Aut} (P)\cdot x=\{g(x):g\in \operatorname {Aut} (P)\}\;(x\in P)$,

welche durch die Operation

$\operatorname {Aut} (P)\times P\to P\;,\;(g,x)\mapsto g\cdot x=g(x)$

der Automorphismengruppe $\operatorname {Aut} (P)$ auf $P$ entstehen.

Weiter sei

${\mathcal {C}}\subseteq 2^{P}$

die Menge der Ketten innerhalb $P$, also die Menge aller Teilmengen von $P$ mit der Eigenschaft, dass für je zwei darin enthaltene Elemente $x,y$ stets die Relation $x\leq y$ oder die Relation $y\leq x$ erfüllt ist.

Schließlich sei

${\mathcal {A}}\subseteq 2^{P}$

die Menge der Antiketten innerhalb $P$, also die Menge aller Teilmengen von $P$ mit der Eigenschaft, dass für je zwei darin enthaltene Elemente $x,y$ niemals die Relation $x<y$ erfüllt ist.

Formulierung des Charakterisierungssatzes

Unter den oben genannten Voraussetzungen gilt:

(A) Jeder der Orbits $O_{i}\;(i=1,\dots ,t)$ ist eine Antikette von $P$:

${\mathcal {O}}\subseteq {\mathcal {A}}$ .

(B) Die folgenden vier Bedingungen sind gleichwertig:

(B1)

Für $A\in {\mathcal {A}}$ gilt stets

$\sum _{i=1}^{t}{\frac {|O_{i}\cap A|}{|O_{i}|}}\leq 1$.

(B2)

Jeder der Orbits $O_{i}\;(i=1,\dots ,t)$ ist eine maximale Antikette, wird also von keiner anderen Antikette von $P$ echt umfasst.

(B3)

In $P$ existiert eine Kette, welche zugleich ein Repräsentantensystem der durch die Orbitmenge ${\mathcal {O}}$ gegebenen Partition

$P=O_{1}{\dot {\cup }}O_{2}{\dot {\cup }}\,\dots {\dot {\cup }}O_{t}$

darstellt.

(B4)

Für jede Funktion $w\colon P\rightarrow \mathbb {R}$, bei der sämtliche Restriktionen $w{\upharpoonright }O$ konstante Funktionen sind, gilt

$\max _{A\in {\mathcal {A}}}\;{w[A]}=\max _{i=1,\dots ,t}\;{w[O_{i}]}$.

Beweis des Charakterisierungssatzes

Ad (A)

Die Annahme, es würde für $x\in P$ und $g\in \operatorname {Aut} (P)$

(1) $x<g(x)$

gelten, führt mittels Iteration zu der Ungleichungskette

(2) $x<g(x)<g^{2}(x)<g^{3}(x)<\ldots <g^{n}(x)<g^{n+1}(x)<\ldots \ (\forall n\in \mathbb {N} )$ .

Da $P$ endlich ist, jede solche Kette jedoch unendlich, kann (2) nicht gelten und damit ebenso wenig (1).

Folglich ist jeder $\operatorname {Aut} (P)$-Orbit eine Antikette von $P$ .

Ad (B)

Der Beweis wird in einem Ringschluss geführt. Dazu sei $I=\{1,\dots ,t\}$ .

(B1) → (B2)

Wenn eine Teilmenge $X\subseteq P$ einen Orbit $O_{h}$ echt umfasst, so gilt

(3) $X\supseteq {O_{h}\;{\dot {\cup }}\;\{y\}}$

für mindestens ein $y\in O_{j}$ zu einem Orbit $O_{j}\neq O_{h}$ .

Also folgt

(4) $\sum _{i=1}^{t}{\frac {|O_{i}\cap X|}{|O_{i}|}}\geq {\frac {|O_{h}|}{|O_{h}|}}+{\frac {1}{|O_{j}|}}\geq 1+{\frac {1}{|O_{j}|}}>1$.

Durch (4) ist die Ungleichung von (B1) verletzt, weswegen im Falle der Gültigkeit von (B1) keine solches $X\subseteq P$ noch Antikette von $P$ sein kann.

Schritt 1

Man definiert zunächst eine Hilfsfunktion $\Gamma$, die sich infolge der Tatsache ergibt, dass beliebiges $x\in P$ stets mindestens ein $C\in {\mathcal {C}}$  

- nämlich $C=\{x\}$   -

existiert, so dass

(4) $x\in C\;,\;\max(C)=x$

erfüllt ist.

Also ist vermöge

(5) $\Gamma \colon P\to \mathbb {N} \;;\;x\mapsto \Gamma (x):=\max {\bigl (}\{|C|\colon C\in {\mathcal {C}}\;,\;x\in C\;,\;\max(C)=x\}{\bigr )}\;(x\in P)$

eine sinnvoll erklärte Funktion gegeben.

Nun ist die Bildmenge $\Gamma (P)$ eine nichtleere Teilmenge der natürlichen Zahlen und daher kann man ihre Mächtigkeit abschätzen wie folgt:

(6) $|\Gamma (P)|\leq \max(\Gamma (P))$.

Gemäß (5) ergibt sich aus (6) sofort

(7) $|\Gamma (P)|\leq \max(\{|C|\colon C\in {\mathcal {C}}\})$ .

An dieser Stelle ist die wesentliche Tatsache zu berücksichtigten, dass eine Kette und eine Antikette von $P$ stets allerhöchstens ein einziges Element gemeinsam haben.

Deswegen ist vermöge (A) für $C\in {\mathcal {C}}$ stets die Abschätzung

(8) $|O_{i}\cap C|\leq 1\;(i\in I)$

gegeben.

Da andererseits die Orbits eine Partition von $P$ bilden, zieht (8) durchgängig die wichtige Beziehung

(9) $|C|=\sum _{i=1}^{t}{|O_{i}\cap C|}\leq t\;(C\in {\mathcal {C}})$

nach sich.

Verbindet man (7) und (9), so hat man die Ungleichungskette

(10) $|\Gamma (P)|\leq \max(\{|C|\colon C\in {\mathcal {C}}\})\leq t$ .

Schritt 2

Es genügt zum Schluss auf (B3) zu zeigen, dass bei Voraussetzung von (B2) stets die Identität

(11) $|\Gamma (P)|=t$

besteht.

Denn:

Aus (11) ergibt sich dann in Verbindung mit (10) zunächst

(12) $\max _{C\in {\mathcal {C}}}{|C|}=t$.

Da nun $P$ endlich, zieht (12) in Verbindung mit (9) nach sich, dass ein $C\in {\mathcal {C}}$ existiert, für das in (8) stets das Gleichheitszeichen gilt.

Das aber heißt:

Es gibt in $P$ eine Kette, welche zugleich ein Repräsentantensystem für die Orbitmenge ${\mathcal {O}}$ darstellt.

Schritt 3

Zur Vollendung des Beweises von (B2) → (B3) bleibt also die Identität (11) zu zeigen.

Dazu sei

(13) $n_{0}\in \Gamma (P)$ und $P_{n_{0}}=\{x\in P\colon \Gamma (x)=n_{0}\}$ .

$P_{n_{0}}$ ist offenbar eine Antikette von $P$ und zudem nicht die leere Menge.

Man wählt nun irgendein $p\in P_{n_{0}}$ .

Jetzt wird bedeutsam, dass jedes $g\in \operatorname {Aut} (P)$ und ebenso die zugehörige inverse Abbildung $g^{-1}$ die Ordnungsstruktur von $P$ streng erhalten.

Das bedeutet:

Es entsprechen unter $g$ diejenigen Ketten, in denen $p$ das Maximum ist, umkehrbar eindeutig denjenigen Ketten, in denen $g(p)$ das Maximum ist.

Dies zieht die Gleichung

(14) $\Gamma (g(p))=\Gamma (p)=n\;(g\in \operatorname {Aut} (P))$

nach sich.

(14) wiederum bedeutet, dass der Orbit, dem $p$ angehört, etwa $O_{i_{p}}$, ganz in $P_{n_{0}}$ enthalten ist:

(15) $O_{i_{p}}\subseteq P_{n_{0}}$ .

Nun kommt die vorausgesetzte Bedingung (B2) zur Wirkung. Derzufolge kann in (15) nicht die strenge Inklusion gelten.

Man hat also sogar die Identität

(16) $O_{i_{p}}=P_{n_{0}}$ .

Ganz gleichartige Überlegungen lassen sich jedoch für alle $n\in \Gamma (P)$ anstellen. Folglich gilt insgesamt

(17) $\{P_{n}\colon n\in \Gamma (P)\}\subseteq {\mathcal {O}}$ .

Nun ist auch $\{P_{n}\colon n\in \Gamma (P)\}$ eine Partition von $P$ und zwei Partitionen einer Menge können einander niemals echt umfassen.

Daher verschärft sich (17) zu der Identität

(18) $\{P_{n}\colon n\in \Gamma (P)\}={\mathcal {O}}$ .

Mit (18) jedoch gilt dann auch die Identität

(19) $|\Gamma (P)|=|\{P_{n}\colon n\in \Gamma (P)\}|=|{\mathcal {O}}|$ .

Die Identität (19) wiederum impliziert die Identität (11) und diese war zu zeigen.

(B3) → (B4)

Es sei $w$ eine reellwertige Funktion, bei der sämtliche Restriktionen $w{\upharpoonright }O$ konstante Funktionen sind. Für ein solches $w$ ist zum Nachweis der Identität (B4) in zwei Schritten zu beweisen, dass dort sowohl von links nach rechts als auch von rechts nach links die entsprechenden Ungleichungen gelten.

Schritt 1

Der erste Schritt ist sehr einfach. Denn es gilt (A) und daher ist selbstverständlich

(20) $\max _{A\in {\mathcal {A}}}\;{w[A]}\geq \max _{i\in I}\;{w[O_{i}]}$ .

Schritt 2

Also bleibt zum Nachweis von (B4) allein die zu (20) duale Ungleichung herzuleiten.

Dazu sei $A$ eine beliebige Antikette $A\in {\mathcal {A}}$. Hierfür ist die Ungleichung

(21) $w[A]\leq \max _{i\in I}\;{w[O_{i}]}$

zu zeigen.

Dies geschieht durch Anwendung des Korollars zur verallgemeinerten LYM-Ungleichung.

Dazu wird zunächst einbezogen, dass gemäß Voraussetzung in $P$ eine Kette

(22) $C=\{c_{1},\dots ,c_{t}\}\;{\text{mit}}\;\{c_{i}\}=O_{i}\cap C\;(i\in I)$

enthalten ist.

Es ist damit für $i\in I$ stets

(23) $O_{i}=\operatorname {Aut} (P)\cdot c_{i}$

gültig und daher für jedes $x\in O_{i}$ aufgrund der Beschaffenheit von $w$ in Verbindung mit (22) und (23) durchgängig

(24) $w(x)=w(c_{i})={\frac {w[O_{i}]}{|\operatorname {Aut} (P)\cdot c_{i}|}}$.

Wegen der Partitionseigenschaften von ${\mathcal {O}}$ folgt nun aus (24) sogleich

(25) ${\begin{aligned}w[A]&=\sum _{i\in I}\;{w[O_{i}\cap A]}\\&=\sum _{i\in I}\;{|{\operatorname {Aut} (P)\cdot c_{i}}\cap A|\cdot w(c_{i})}\\&=\sum _{i\in I}\;{{\frac {|{\operatorname {Aut} (P)\cdot c_{i}}\cap A|}{|\operatorname {Aut} (P)\cdot c_{i}|}}\cdot w[O_{i}]}\\\end{aligned}}$ .

An dieser Stelle ist zu berücksichtigen, dass für jeden Automorphismus $g\in \operatorname {Aut} (P)$ mit $C$ auch stets $g(C)$ eine Kette von $P$ ist.

Folglich gilt wegen der Antiketteneigenschaft von $A$ stets

(26) $|g(C)\cap A|\leq 1$ .

Es kann also immer nur höchstens einen einzigen Index $i\in I$ geben mit $g(c_{i})\in A$.

Somit folgt schließlich aus (25) und (26) durch Anwendung des Korollars zur verallgemeinerten LYM-Ungleichung die Ungleichung (21) und damit (B4).

(B4) → (B1)

Vermöge

(27) $v\colon P\to \mathbb {R} \;;\;x\mapsto \ v(x):={\frac {1}{|\{g(x):g\in \operatorname {Aut} (P)\}|}}\;(x\in P)$

ist eine reelwertige Funktion auf $P$ erklärt, welche die in (B4) genannte Eigenschaft hat.

Denn es ist offenbar für $i\in I$ und $x\in O_{i}$ durchgängig

(28) $v(x):={\frac {1}{|O_{i}|}}$ .

Folglich ist für $i\in I$ stets

(29) $v[O_{i}]=|O_{i}|\cdot {\frac {1}{|O_{i}|}}=1$.

Damit aber erhält man unter der Voraussetzung von (B4) für jede Antikette $A\in {\mathcal {A}}$

(30) ${\begin{aligned}\sum _{i=1}^{t}{\frac {|O_{i}\cap A|}{|O_{i}|}}&=\sum _{i\in I}\;{|O_{i}\cap A|\cdot {\frac {1}{|O_{i}|}}}\\&=\sum _{i\in I}\;{v[O_{i}\cap A]}\\&=v[A]\\&\leq \max _{i\in I}\;{v[O_{i}]}\\&=1\\\end{aligned}}$ .

Mit (30) jedoch hat man (B1) .

Normale geordnete Mengen

Der Ausgangspunkt sind hier die beiden Spernerschen Ungleichungen, welche Emanuel Sperner selbst in seinem 1928-er Artikel als wesentliche Argumentationshilfe benutzt. Von ihnen lässt sich zeigen, dass sie logisch äquivalent zur LYM-Ungleichung sind.

Setzt man dies in den weiteren Rahmen der Ordnungstheorie, so gelangt man zu den normalen geordneten Mengen (engl. normal posets). Charakteristische Eigenschaft der normalen geordneten Mengen ist die (in der englischsprachigen Literatur) sogenannte normalized matching property , welche als Übertragung der beiden Spernerschen Ungleichungen in den Rahmen der endlichen geordneten Mengen mit Rangfunktion (englisch rank function) zu betrachten ist. Es lässt sich zeigen, dass beide Ungleichungen in diesem Rahmen mit der LYM-Ungleichung gleichwertig ist. In der englischsprachigen Literatur spricht man hier - in einem etwas anderen Sinne als oben! - dann auch von der LYM-Eigenschaft (engl. LYM property). Einen umfassenden Überblick über diesen Zweig der Spernertheorie geben die beiden Monographien von Anderson und von Engel sowie die beiden Übersichtsartikel von Greene / Kleitman und von West .

Quellen

Artikel und Originalarbeiten

• R. Ahlswede, Z. Zhang: An identity in combinatorial extremal theory. In: Advances in Mathematics. Band 80, 1990, S. 137–151. MR1046687
• R. Ahlswede, N. Cai: A generalization of the AZ identity. In: Combinatorica. Band 13, 1993, S. 241–247.  MR1238819

• Douglas B. West: Extremal problems in partially ordered sets in : Ivan Rival (ed.): Ordered Sets. Proceedings of the NATO advanced study institute held at Banff, Canada, August 28 to September 12, 1981. D. Reidel Publishing Company, Dordrecht [u.a.] 1982, ISBN 90-277-1396-0, S. 473–521.  MR0661304

• Béla Bollobás: On generalized graphs. Acta Mathematica Academiae Scientiarum Hungaricae, Vol. 16, 3–4, (1965): 447–452. doi:10.1007/BF01904851, MR0183653

• Curtis Greene and Daniel J. Kleitman: Proof techniques in the theory of finite sets in : G. C. Rota (ed.): Studies in Combinatorics. Mathematical Association of America, Washington, DC 1978, ISBN 0-88385-117-2, S. 23–79.  MR0513002

• D. J. Kleitman: On an extremal property of antichains in partial orders. The LYM property and some of its implications and applications in : M. Hall and J. H. van Lint (eds.): Combinatorics (Math. Centre Tracts 55). Amsterdam 1974, S. 77–90.  MR0360379

• D. Lubell: A short proof of Sperner's lemma. Journal of Combinatorial Theory, Vol. 1, 2 (1966): 299. doi:10.1016/S0021-9800(66)80035-2, MR0194348

• L.D. Meshalkin: Generalization of Sperner's theorem on the number of subsets of a finite set. Theory of Probability and its Applications, Vol. 8, 2 (1963): 203–204. doi:10.1137/1108023, MR0150049

• Hans-Josef Scholz: Über die Kombinatorik der endlichen Potenzmengen im Zusammenhang mit dem Satz von Sperner. Dissertation, Universität Düsseldorf (1987).

• Emanuel Sperner: Ein Satz über Untermengen einer endlichen Menge. Math. Z. 27 (1928): 544–548. MR1544925

• Koichi Yamamoto: Logarithmic order of free distributive lattice. Journal of the Mathematical Society of Japan, Vol. 6 (1954): 343–353. MR0067086.

Monographien

• Martin Aigner: Kombinatorik II: Matroide und Transversaltheorie (= Hochschultext). Springer Verlag, Berlin (u. a.) 1976, ISBN 3-540-07949-1.  MR0460127

• Martin Aigner: Combinatorial Theory (= Grundlehren der Mathematischen Wissenschaften. Band 234). Springer Verlag, Berlin (u. a.) 1979, ISBN 3-540-90376-3.  MR0542445

• Martin Aigner: Diskrete Mathematik (= Dokumente zur Geschichte der Mathematik. Band 6). 6. Auflage. Vieweg Verlag, Wiesbaden 2006, ISBN 978-3-8348-0084-8.  MR1085963

• Ian Anderson: Combinatorics of Finite Sets. Clarendon Press, Oxford 1987, ISBN 0-19-853367-5.  MR0892525

• Konrad Engel: Sperner Theory (= Encyclopedia of Mathematics and its Applications. Band 65). Cambridge University Press, Cambridge (u. a.) 1997, ISBN 0-521-45206-6.  MR1429390

• Egbert Harzheim: Ordered Sets (= Advances in Mathematics. Band 7). Springer Verlag, New York, NY 2005, ISBN 0-387-24219-8.  MR2127991

• Joseph P. S. Kung, Gian-Carlo Rota, Catherine H. Yan: Combinatorics: The Rota Way. Cambridge University Press, Cambridge (u. a) 2009, ISBN 978-0-521-73794-4.  MR2483561

• Stasys Jukna: Extremal Combinatorics (= Texts in Theoretical Computer Science). Springer Verlag, Heidelberg (u. a.) 2011, ISBN 978-3-642-17363-9.  MR2865719

Weblinks

• Lectures on extremal set systems and two-colorings of hypergraphs (PDF; 237 kB) von Gy. Károlyi.
• Kombinatorische Methoden in der Informatik. (PDF; 1,4 MB) Skript einer Vorlesung von Prof. Dr. Peter Hauck, Uni Tübingen, SS 2008.
• Artikel von Rudolf Ahlswede und Ning Cai zur AZ-Identität
• Artikel von T. D. Thu zur AZ-Identität

Der Satz von Poincaré-Bohl impliziert den Satz von Poincaré-Brouwer!

Der Satz von Poincaré-Bohl, englisch Poincaré-Bohl theorem, ist ein Lehrsatz aus dem mathematischen Teilgebiet der Topologie, welcher den beiden Mathematikern Henri Poincaré (1854–1912) und Piers Bohl (1865–1921) zugerechnet wird. Der Satz behandelt eine grundlegende Eigenschaft des brouwerschen Abbildungsgrades für stetige Vektorfelder im euklidischen Raum.

Der Satz von Poincaré-Bohl besagt:

Gegeben seien eine offene und beschränkte Menge $\Omega \subset \mathbb {R} ^{n}\;(n\in \mathbb {N} )$ und dazu zwei stetige Abbildungen

$F,G\colon {\overline {\Omega }}\to \mathbb {R} ^{n}$   .

Hierzu sei

$\gamma =\partial {\Omega }$

die zugehörige Menge der Randpunkte sowie

$U:=\bigcup _{x\in \gamma }[F(x)\;,\;G(x)]$

die Menge aller Punkte, welche auf den Verbindungsstrecken zwischen $F$- und $G$-Bildpunkt dieser Randpunkte liegen.

Dann gilt:

Für jeden außerhalb liegenden Punkt, also für jeden Punkt $y\in \mathbb {R} ^{n}\setminus U$, stimmen die brouwerschen Abbildungsgrade von $F$ und $G$ überein:

$d(F,\Omega ,y)=d(G,\Omega ,y)$   .

Durch einige elementare Schlussfolgerungen - und im Anschluss an die Darstellung von Egbert Harzheim - lässt sich nun zeigen, dass aus dem Satz von Poincaré-Bohl durch Anwendung der Eigenschaften des Abbildungsgrades und eines einfachen gemetrischen Hilfssatzes unmittelbar der berühmte Satz von Poincaré-Brouwer folgt, welcher folgendes besagt:

Für jedes $m\in \mathbb {N}$ und für jede stetige Abbildung $f\colon \mathbb {S} ^{2m}\to \mathbb {R} ^{2m+1}$ existiert ein $x_{0}\in \mathbb {S} ^{2m}$ und ein $\lambda \in \mathbb {R}$ mit $f(x_{0})=\lambda \cdot x_{0}$.

Beweis der Folgerung

Für den Beweis benötigt man einen Hilfssatz.

Hilfssatz

Enthält im $\mathbb {R} ^{k+1}\;(k\in \mathbb {N} )$ eine Sehne $[a\;,\;b]\;(a\;,\;b\in \mathbb {S} ^{k})$ der abgeschlossenen Einheitskugel ${\overline {B_{\mathbb {R} ^{k+1}}}}$ den Nullpunkt , so ist die Sehne $[a\;,\;b]$ ein Durchmesser mit antipodischen Endpunkten $a=-b$.

Der Beweis des Hilfssatzes geht wie folgt:

Nach Voraussetzung gilt für ein $t\in \mathbb {R} \;,\;0\leq t\leq 1$:

$\mathbf {0} =ta+(1-t)b$

und damit

$ta=-(1-t)b$   (*)

und weiter

$t^{2}=(\;t\;\|a\|_{2}\;)^{2}=(\;\|ta\|_{2}\;)^{2}=(\;\|-(1-t)b\|_{2}\;)^{2}=(\;(1-t)\|b\|_{2}\;)^{2}=(1-t)^{2}=1-2t+t^{2}$   .

Also ist

$0=1-2t$

und damit

$t={\frac {1}{2}}$   .

Wegen (*) folgt dann sogleich

$a=-b$   .

Eigentlicher Beweis

Für den Fall, dass $f$ eine Nullstelle hat, ist die Behauptung unmittelbar einsichtig.

Andernfalls betrachtet man zu $f$ die folgende auf der abgeschlossenen Einheitskugel von $\mathbb {R} ^{2m+1}$ definierte stetige Abbildung:

$F\colon {\overline {B_{\mathbb {R} ^{2m+1}}}}\to {\overline {B_{\mathbb {R} ^{2m+1}}}}\subset \mathbb {R} ^{2m+1}$

mit

$F(x)={\begin{cases}{\frac {\|x\|_{2}}{\|f{({\frac {x}{\|x\|_{2}}})}\|_{2}}}\cdot f{({\frac {x}{\|x\|_{2}}})}&{\text{, falls }}x\in {\overline {B_{\mathbb {R} ^{2m+1}}}}\setminus \{0\}\\0&{\text{, falls }}x=0\end{cases}}$   .

Nun ist

$\mathbb {S} ^{2m}=\partial {\overline {B_{\mathbb {R} ^{2m+1}}}}$

und daher ist es nach dem Satz von Poincaré-Bohl unmöglich, dass

$0\notin \bigcup _{x\in \mathbb {S} ^{2m}}{\bigl (}[F(x)\;,\;x]\cup [F(x)\;,\;-x]{\bigr )}={\bigl (}\bigcup _{x\in \mathbb {S} ^{2m}}{[F(x)\;,\;x]}{\bigr )}\cup {\bigl (}\bigcup _{x\in \mathbb {S} ^{2m}}{[F(x)\;,\;-x]}{\bigr )}$

gilt.

Denn dann wäre ja mit der Inklusionsabbildung

$I\colon {\overline {B_{\mathbb {R} ^{2m+1}}}}\to \mathbb {R} ^{2m+1}\;,\;x\mapsto x$

und der Antipodenabbildung

$A\colon {\overline {B_{\mathbb {R} ^{2m+1}}}}\to \mathbb {R} ^{2m+1}\;,\;x\mapsto -x$

die Gleichung

$1=d(I,{\overline {B_{\mathbb {R} ^{2m+1}}}},0)=d(A,{\overline {B_{\mathbb {R} ^{2m+1}}}},0)=(-1)^{2m+1}=-1$

gegeben, also ein Widerspruch!

Es ergibt sich also:

Für mindestens ein $x\in \mathbb {S} ^{2m}$ muss

$0\in [F(x)\;,\;x]\cup [F(x)\;,\;-x]$

gelten und folglich

$0\in [F(x)\;,\;x]$   oder   $0\in [F(x)\;,\;-x]$   . (**)

Nun ist stets

$\|F(x)\|_{2}=1\;(x\in \mathbb {S} ^{2m})$

und daher stellt jede der beiden Verbindungsstrecken

$[F(x)\;,\;x]$ und $[F(x)\;,\;-x]$ für $x\in \mathbb {S} ^{2m}$

eine Sehne der Einheitskugel dar.

Nach obigem Hilfssatz folgt aus (**) daher:

Es ist $F(x)=\mp \;x$   für mindestens ein $x\in \mathbb {S} ^{2m}$   .

Wegen $\|x\|_{2}=1$ bedeutet dies aber:

${\frac {1}{\|f{(x)}\|_{2}}}\cdot f(x)=\mp \;x$

und daher

$f(x)=\mp \;{\|f{(x)}\|_{2}}\cdot x$  .

Indem man

$\lambda =\mp \;{\|f{(x)}\|_{2}}$

gemäß (**) passend setzt, hat man alles gezeigt.

Quellen und Hintergrundliteratur

• P. Alexandroff, H. Hopf: Topologie. Erster Band (Reprint) (= Die Grundlehren der mathematischen Wissenschaften. Band 45). Chelsea Publishing Company, New York 1965. 
• Egbert Harzheim: Einführung in die Kombinatorische Topologie (= DIE MATHEMATIK. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X.  MR0533264
• James M. Ortega, W. C. Rheinboldt: Iterative Solution of Nonlinear Equations in Several Variables. (Unabridged republication of the work first published by Acadmic Press, New York and London, 1970) (= Classics in Applied Mathematics. Band 30). Society for Industrial and Applied Mathematics, Philadelphia 2000, ISBN 0-89871-461-3.  MR1744713

Einzelnachweise und Fußnoten

Kreferences />

KKKategorie:Topologie]] KKKategorie:Algebraische Topologie]] KKKategorie:Satz (Mathematik)|Poincaré-Bohl]]

Kreisesatz von Gerschgorin

!!:Beweisarchiv: Lineare Algebra: TOPNAV}} Das Kreisesatz von Gerschgorin oder auch Kreissatz von Gerschgorin bzw. Satz von Gerschgorin, in englischsprachigen Quellen auch Gershgorin circle theorem genannt, ist ein Lehrsatz des mathematischen Teilgebiets der Linearen Algebra. Der Satz ist benannt nach dem weißrussischen Mathematiker Semjon Aronowitsch Gerschgorin und gibt Aufschluss über die Lage der Eigenwerte komplexwertiger Matrizen innerhalb der gaußschen Zahlenebene .

Formulierung des Satzes

Der Satz besagt folgendes:

Es sei

$A=(a_{jk})_{j,k=1,\ldots ,n}\in {\mathbb {C} }^{n\times n}$

eine komplexwertige Matrix $n\times n$-Matrix zu einer natürlichen Zahl $n$ . Dabei sei für jeden der Indizes $j=1,\ldots ,n$

$c_{j}=\sum _{k=1,\ldots ,n \atop \;\ k\neq j}{|a_{jk}|}$

und dazu

$D_{j}={\overline {U_{c_{j}}\,(a_{jj})}}=\{z\in \mathbb {C} \colon |a_{jj}-z|\leq c_{j}\}$

die abgeschlossene Kreisscheibe mit Radius $c_{j}$ und Mittelpunkt $a_{jj}$.

Dann gilt:

Zu jedem komplexen Eigenwert $\lambda$ der Matrix $A$ gibt es eine Kreisscheibe $D_{j}\;(j=1,\ldots ,n)$, die $\lambda$ enthält.

Beweis des Satzes

Der Darstellung von Ortega und Rheinboldt folgend lässt sich der Beweis führen wie folgt:

Sei

$\lambda \in \mathbb {C}$

Eigenwert der Matrix

$A\in {\mathbb {C} }^{n\times n}$

und sei

$x\in {\mathbb {C} }^{n}\setminus \{0\}$

ein zugehöriger Eigenvektor und

$B=A-\lambda I_{n}$

mit

$I_{n}\in {\mathbb {C} }^{n\times n}$

als komplexwertiger $n\times n$-Einheitsmatrix.

Dann gilt einerseits

$Bx=0$

und andererseits wegen $x\neq 0$ für einen Index $m\in \{1,\ldots ,n\}$

$|x_{m}|=\max _{k=1,\ldots ,n}{|x_{k}|}>0$.

Man hat also

$0=\sum _{k=1,\ldots ,n}{b_{mk}x_{k}}$

und dann weiter

$|x_{m}|\cdot |b_{mm}|=|b_{mm}x_{m}|=|-\sum _{k=1,\ldots ,n \atop \;\ k\neq m}{b_{mk}x_{k}}|\leq |x_{m}|\cdot \sum _{k=1,\ldots ,n \atop \;\ k\neq m}|{b_{mk}}|$.

und damit

$|x_{m}|\cdot |a_{mm}-\lambda |\leq |x_{m}|\cdot \sum _{k=1,\ldots ,n \atop \;\ k\neq m}|{a_{mk}}|=|x_{m}|\cdot c_{m}$ .

Folglich ist

$|a_{mm}-\lambda |\leq c_{m}$

und daher

$\lambda \in D_{m}$   ,

was die Behauptung des Satzes beweist.

Quellen und Hintergrundliteratur

• S. Gerschgorin: Uber die Abgrenzung der Eigenwerte einer Matrix. In: Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya. Band 1, 1931, S. 749–754 ([2]). 
• James M. Ortega, W. C. Rheinboldt: Iterative Solution of Nonlinear Equations in Several Variables (= Classics in Applied Mathematics. Band 30). Society for Industrial and Applied Mathematics, Philadelphia 2000, ISBN 0-89871-461-3 ((Unabridged republication of the work first published by Acadmic Press, New York and London, 1970)).  MR1744713
• Richard S. Varga: Geršgorin and His Circles (= Springer Series in Computational Mathematics. Band 36). Springer Verlag, Berlin 2004, ISBN 3-540-21100-4.  MR2093409

Einzelnachweise

rreferences />

KKKategorie:Lineare Algbra]] KKKategorie:Matrix]] KKKategorie:Satz (Mathematik)|Gerschgorin, Kreisesatz von]]

Zu den Schwerpunktsätzen von Leibniz

Die beiden Schwerpunktsätze von GOTTFRIED WILHELM LEIBNIZ sind in der euklidischen Geometrie angesiedelt und geben eine allgemeine Formel an, welche erlaubt, in der Ebene bzw. im Raum für einen gegebenen Punkt und ein gegebenes Vieleck (Dreieck bzw. Tetraeder) die Abstände des Punktes von den Eckpunkten in Beziehung zu setzen zu den Abständen der Eckpunkte vom Schwerpunkt des Vielecks.

Im Einzelnen gilt dabei für einen beliebigen Punkt $X$ in der Ebene bzw. im Raum:

(1) Ist $P$ der geometrische Schwerpunkt eines Dreiecks mit den Eckpunkten $A,B,C$, so ist

$|A-X|^{2}+|B-X|^{2}+|C-X|^{2}=3\cdot |P-X|^{2}+|A-P|^{2}+|B-P|^{2}+|C-P|^{2}$   .

(2) Ist $P$ der geometrische Schwerpunkt eines Tetraeders mit den Eckpunkten $A,B,C,D$, so ist

$|A-X|^{2}+|B-X|^{2}+|C-X|^{2}+|D-X|^{2}=4\cdot |P-X|^{2}+|A-P|^{2}+|B-P|^{2}+|C-P|^{2}+|D-P|^{2}$   .

Die beiden Schwerpunktsätze erlauben eine naheliegende Verallgemeinerung, welche in jedem reellen Skalarproduktraum und insbesondere in jedem reellen Hilbertraum ${\mathcal {H}}$ Gültigkeit hat. Wie sich zeigt, beruht diese Verallgemeinerung wesentlich auf der folgenden binomische Identitätsgleichung:

$|X-Y|^{2}=|X|^{2}-2\cdot \langle X\;,\;Y\rangle +|Y|^{2}\;\;(X,Y\in {\mathcal {H}})$

Formulierung der Verallgemeinerung

Für eine natürliche Zahl $n$ seien in einem reellen Skalarproduktraum ${\mathcal {H}}$   $n+2$ Punkte $A_{1},\ldots ,A_{n},P,X$ gegeben.

Dabei habe der Punkt $P$ in Bezug auf die Punkte $A_{j}\;(j=1,\ldots ,n)$ die affine Darstellung

$P=\sum _{j=1}^{n}{{\alpha }_{j}A_{j}}$

mit

${\alpha }_{j}\in \mathbb {R} \;(j=1,\ldots ,n)$

und

$\sum _{j=1}^{n}{{\alpha }_{j}}=1$   .

Dann gilt die Identität :

(1) $\sum _{j=1}^{n}{{\alpha }_{j}\cdot |A_{j}-X|^{2}}-|P-X|^{2}=\sum _{j=1}^{n}{{\alpha }_{j}\cdot |A_{j}-P|^{2}}$

Ist insbesondere $P$ der geometrische Schwerpunkt der Punkte $A_{j}$,

ist also

$P={\frac {1}{n}}\sum _{j=1}^{n}{A_{j}}$   ,

so gilt sogar

(2) $\sum _{j=1}^{n}{|A_{j}-X|^{2}}=n\cdot |P-X|^{2}+\sum _{j=1}^{n}|A_{j}-P|^{2}=\sum _{j=1}^{n}{\bigl (}|P-X|^{2}+|A_{j}-P|^{2}{\bigr )}$   .

Beweis der Verallgemeinerung

Da die Behauptung translationsinvariant ist, kann man annnehmen, dass $X=\mathbf {0}$ ist.

Da aus zudem (2) offenbar unmittelbar als Anwendung von (1) folgt, ist demnach allein zu zeigen:

(1*) $\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}|^{2}-|P|^{2}=\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}-P|^{2}$

Dies tut man, indem man von rechts nach links umformt.

So erhält man:

${\begin{aligned}\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}-P|^{2}&=\sum _{j=1}^{n}{\alpha }_{j}\cdot {\bigl (}|A_{j}|^{2}-2\cdot \langle A_{j}\;,\;P\rangle +|P|^{2}{\bigr )}\\&=\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}|^{2}-2\cdot \sum _{j=1}^{n}{\alpha }_{j}\cdot \langle A_{j}\;,\;P\rangle +\sum _{j=1}^{n}{\alpha }_{j}\cdot |P|^{2}\\&=\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}|^{2}-2\cdot \langle \sum _{j=1}^{n}{\alpha }_{j}\cdot A_{j}\;,\;P\rangle +1\cdot |P|^{2}\\&=\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}|^{2}-2\cdot \langle P\;,\;P\rangle +1\cdot |P|^{2}\\&=\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}|^{2}-2\cdot |P|^{2}+1\cdot |P|^{2}\\&=\sum _{j=1}^{n}{\alpha }_{j}\cdot |A_{j}|^{2}-|P|^{2}\\\end{aligned}}$

Hintergrundliteratur

• Heinrich Dörrie: Mathematische Miniaturen. Sändig (u.a.), Wiesbaden 1979, ISBN 3-500-21150-X (Zweiter unveränderter Nachdruck der Ausgabe von 1943). 
• Max Koecher, Aloys Krieg: Ebene Geometrie (= Springer-Lehrbuch). 2., neu bearbeitete und erweiterte Auflage. Springer Verlag, Berlin (u.a.) 2000, ISBN 3-540-67643-0. 

Einzelnachweise und Fußnoten

Kreferences />

KKKategorie:Geometrie]] KKKategorie:Ebene Geometrie]] KKKategorie:Satz (Mathematik)|Leibniz, Satz von (Euklidische Geometrie)]]

Analogon zum Satz von Baire für endlich viele abgeschlossene Teilmengen

Formulierung des Analogons

Gegeben seien ein topologischer Raum $X$ und eine endliche Indexmenge $I\neq \emptyset$ und dazu eine endliche Familie $(E_{i})_{i\in I}$ von abgeschlossenen Teilmengen $E_{i}\subseteq X$ mit

$V=\bigcup _{i\in I}{E_{i}}$

als Vereinigungsmenge dieser abgeschlossenen Teilmengen.

Dann gilt:

Ist das Innere $V^{\circ }\neq \emptyset$ , so ist sogar schon für eine der Teilmengen $E_{i}$ das Innere ${E_{i}}^{\circ }\neq \emptyset$.

Beweis

Der Beweis wird mit vollständiger Induktion geführt. Es sei o. B. d. A.

$I=\{1,2,\ldots ,n\}$ vorausgesetzt.

Induktionsanfang

$|I|=n=1$

Hier ist nichts zu zeigen.

Induktionsschritt

Sei $|I|=n>1$ und sei die Aussage schon bewiesen für alle $(n-1)$-elementigen Indexmengen.

Zwischenschritt $|I|=n=2$

Hier gilt also

$V=E_{1}\cup E_{2}$

und dabei

$U:={(E_{1}\cup E_{2})}^{\circ }\neq \emptyset$.

Nehmen wir an, es sei

${E_{1}}^{\circ }=\emptyset$.

Dann gilt für die in $X$ offene (!) Menge $U\setminus E_{2}$, dass

$U\setminus E_{2}\subseteq E_{1}$

und dann sogar

$U\setminus E_{2}\subseteq {E_{1}}^{\circ }=\emptyset$

sein muss.

Folglich ist dann auch

$U\setminus E_{2}=\emptyset$

und damit

$\emptyset \neq U\subseteq E_{2}$.

Daher muss auch

${E_{2}}^{\circ }\neq \emptyset$

gelten.

Eigentlicher Induktionsschritt

Es ist also nun

$V=(E_{1}\cup E_{2}\cup \cdots \cup E_{n-1})\cup E_{n}$.

Dann ist entweder

${E_{n}}^{\circ }\neq \emptyset$

und es ist nichts weiter zu zeigen.

Oder es gilt nach dem Zwischenschritt und aufgrund der Tatsache, dass die Vereinigung von endlich vielen abgeschlossenen $X$-Teilmengen immer abgschlossen ist,

$(E_{1}\cup E_{2}\cup \cdots \cup E_{n-1})^{\circ }\neq \emptyset$.

Doch nun kommt die Induktionsvoraussetzung zum Tragen, wonach für einen Index $k\in \{1,2,\ldots ,n-1\}$ schon

${E_{k}}^{\circ }\neq \emptyset$

sein muss.

Also ist alles gezeigt.

Folgerungen aus dem Analogon

• (F1) Unter den obigen Voraussetzungen gilt stets

${{\bigl (}{\bigcup _{i\in I}{E_{i}}}{\bigr )}}^{\circ }={{\bigl (}{\bigcup _{j\in I \atop {E_{j}}^{\circ }\neq \emptyset }{E_{i}}}{\bigr )}}^{\circ }$

• (F2) Die zuvor genannte Folgerung (F1) hat auch dann noch Bestand, wenn - bei sonst gleichen Voraussetzungen - die Indexmenge als nicht notwendig endlich, die Familie $(E_{i})_{i\in I}$ jedoch als lokalendliche Familie vorausgesetzt wird. Für eine solche lokalendliche Familie abgeschlossener $X$-Teilmengen gilt das Analogon zum baireschen Satz also in gleicher Weise.

Beweis der Folgerung (F1)

Setzt man

$V:=\bigcup _{i\in I}{E_{i}}$

und

$W:=\bigcup _{j\in I \atop {E_{j}}^{\circ }\neq \emptyset }{E_{i}}$

und

$T:=\bigcup _{j\in I \atop {E_{j}}^{\circ }=\emptyset }{E_{i}}$ ,

so gilt offenbar

$V=W\cup T$ .

Wegen

$V^{\circ }\subseteq V$

folgt dann unmittelbar

$V^{\circ }\setminus W\subseteq T$ .

Andererseits ist gemäß dem Analogon

$T^{\circ }=\emptyset$.

Da zudem $W$ abgeschlossen in $X$ ist, muss $V^{\circ }\setminus W$ offen in $X$ sein und so ergibt sich zusammengenommen

$V^{\circ }\setminus W\subseteq T^{\circ }=\emptyset$ .

Folglich hat man

$V^{\circ }\setminus W=\emptyset$.

und damit auch

$V^{\circ }\subseteq W$

und aus Gründen der Idempotenz sogleich

$V^{\circ }=V^{\circ \circ }\subseteq W^{\circ }$.

Da $W$ Teilmenge von $V$ und das Bilden des Inneren eine monotone Operation ist , gilt die umgekehrte Inklusion ohnehin.

Folglich hat man

$V^{\circ }=W^{\circ }$.

Dies war zu zeigen.

Anmerkung zu Folgerung (F2)

Die Folgerung (F2) beruht darauf, dass ganz allgemein folgendes gilt:

• Ist in einem topologischen Raum $X$ zu einer Indexmenge $I\neq \emptyset$ eine lokalendliche Familie $(E_{i})_{i\in I}$ von $X$-Teilmengen $E_{i}\subseteq X$ gegeben, so ist auch $({\overline {E_{i}}})_{i\in I}$ eine lokalendliche Familie und dabei gilt

${\overline {{\bigl (}{\bigcup _{i\in I}{E_{i}}}{\bigr )}}}=\bigcup _{i\in I}{\overline {E_{i}}}$ .

Hintergrundliteratur

• Horst Schubert: Topologie. 4. Auflage. B. G. Teubner Verlag, Stuttgart 1975, ISBN 3-519-12200-6.  MR0423277

Einfacher Nicht-Existenzsatz für 2-(v,k,λ)-Blockpläne

Formulierung des Satzes

Gegeben sei ein $2{\text{-}}(v,k,\lambda )$-Blockplan mit $1\leq k\leq v-1$.

Dann gilt:

Teil 1

(A1a)Ist $q:=2\lambda -1$ eine Primzahl und zugleich ein Teiler von $v$ und ist weiter $k\equiv r\;({\bmod {\;}}q)$, so ist $\lambda$ eine ungerade Zahl, also $q\equiv 1\;({\bmod {\;}}4)$. Diese Aussage gilt insbesondere für symmetrische $2{\text{-}}(v,k,\lambda )$-Blockpläne.

(A1b) Ist also $\lambda =2$ und $q=3$, so kann, wenn $k\equiv r\;({\bmod {\;}}q)$ gilt, $v$ nicht durch $3$ teilbar sein. Dies gilt speziell für symmetrische $2{\text{-}}(v,k,2)$-Blockpläne, also (gemäß englischer Terminologie) für die biplanes.

(A1c) Insgesamt gibt es im Falle $\lambda =2$ unter den genannten Bedingungen nur die folgenden beiden Möglichkeiten:

$v\equiv 1\;({\bmod {\;}}3)$ und ($k\equiv 0\;({\bmod {\;}}3)$ oder $k\equiv 1\;({\bmod {\;}}3)$)

oder

$v\equiv 2\;({\bmod {\;}}3)$ und $k\equiv 2\;({\bmod {\;}}3)$

.

Teil 2

(A2a)Ist $\lambda \geq 2$ und zugleich $s:=3\lambda -1$ eine Primzahl und dabei $k\equiv r\;({\bmod {\;}}s)$, so kann $s$ nicht zugleich ein Teiler von $v$ sein.

(A2b) Ist dabei sogar $\lambda =2$, also $s=5$, so kann $v$ unter der Bedingung $k\equiv r\;({\bmod {\;}}s)$ nicht durch $5$ teilbar sein. Diese Aussage ist speziell für biplanes richtig.

Teil 3

(A3a)Ist $p:=4\lambda +1$ eine Primzahl und zugleich ein Teiler von $v$ und dabei $k\equiv r\;({\bmod {\;}}p)$, so ist $\lambda$ eine gerade Zahl, also $p\equiv 1\;({\bmod {\;}}8)$.

(A3b) Ist also $\lambda =1$ und damit $p=5$, so kann $v$ unter der Bedingung $k\equiv r\;({\bmod {\;}}s)$ nicht durch $5$ teilbar sein. Diese Aussage ist speziell für projektive Ebenen richtig.

Beweis

Beweis von Teil 1

A1a ergibt sich fast unmittelbar aus der Grundgleichung für Blockpläne

$(v-1)\lambda =r(k-1)$

und algebraischen Umformungen. Aus der Grundgleichung und den Annahmen folgt nämlich

$(v-1)\lambda \equiv (k-1)k\;({\bmod {\;}}q)$.

und damit

$-\lambda \equiv k^{2}-k\;({\bmod {\;}}q)$

und weiter

$-4\lambda \equiv (2k-1)^{2}-1\;({\bmod {\;}}q)$

und weiter

$-2q-1\equiv (2k-1)^{2}\;({\bmod {\;}}q)$

und schließlich

$-1\equiv (2k-1)^{2}\;({\bmod {\;}}q)$.

Die letzte Gleichung besagt nun, dass $-1$ quadratischer Rest bezüglich des Moduls $q$ ist, was mit Hilfe des Legendre-Symbols auch so geschrieben werden kann:

$\left({\frac {-1}{q}}\right)=1$

Nach dem Euler-Kriterium (oder auch nach dem ersten Ergänzungssatz zum quadratischen Reziprozitätsgesetz) ergibt sich damit

$(-1)^{\frac {q-1}{2}}\equiv 1\;({\bmod {\;}}q)$

und schließlich

$(-1)^{\lambda -1}\equiv 1\;({\bmod {\;}}q)$ .

Wegen $q\neq 2$ muss $\lambda -1$ eine gerade Zahl und damit $\lambda$ selbst eine ungerade Zahl sein.

Die Aussagen von A1b und von A1c ergeben sich dann unmittelbar aus der Grundgleichung.

Beweis von Teil 2

Es wird ein Widerspruchsbeweis geführt und dabei ein Wiederspruch abgeleitet daraus, dass $s$ entgegen der Annahme als ein Teiler von $v$ angenommen werde.

Denn dann ergibt sich aus der Grundgleichung

$(v-1)\lambda =r(k-1)$

(mit gleichartigen Rechenschritten wie oben) zunächst

$-4\lambda \equiv (2k-1)^{2}-1\;({\bmod {\;}}s)$

und weiter

$-\lambda \equiv (2k-1)^{2}+3\lambda -1\;({\bmod {\;}}s)$

und weiter

$-\lambda \equiv (2k-1)^{2}\;({\bmod {\;}}s)$

und weiter

$-9\lambda \equiv (6k-2)^{2}\;({\bmod {\;}}s)$

und weiter

$-3s-3\equiv (6k-2)^{2}\;({\bmod {\;}}s)$

und schließlich

$-3\equiv (6k-2)^{2}\;({\bmod {\;}}s)$.

Damit ist (wieder unter Benutzung des Legendre-Symbols)

$\left({\frac {-3}{s}}\right)=1$

und weiter

$\left({\frac {-1}{s}}\right)\left({\frac {3}{s}}\right)=1$

und weiter

$\left({\frac {-1}{s}}\right)\cdot (\left({\frac {3}{s}}\right)\left({\frac {s}{3}}\right))=\left({\frac {s}{3}}\right)$

Daraus folgt mit erstem Ergänzungssatz und quadratischem Reziprozitätsgesetz selbst

$(-1)^{\frac {s-1}{2}}\cdot (-1)^{{\frac {3-1}{2}}\cdot {\frac {s-1}{2}}}=\left({\frac {s}{3}}\right)$

und weiter

$(-1)^{\frac {s-1}{2}}\cdot (-1)^{\frac {s-1}{2}}=\left({\frac {s}{3}}\right)$

und damit

$\left({\frac {s}{3}}\right)=1$

Wegen $s\equiv -1\;({\bmod {\;}}3)$ führt dies zu

$\left({\frac {-1}{3}}\right)=1$

und schließlich zu

$(-1)^{\frac {3-1}{2}}=1$

und damit zum Widerspruch!

Beweis von Teil 3

Wieder ergibt sich aus der Grundgleichung

$(v-1)\lambda =r(k-1)$

(mit gleichartigen Rechenschritten wie oben) zunächst

$-4\lambda \equiv (2k-1)^{2}-1\;({\bmod {\;}}p)$

und weiter

$0\equiv (2k-1)^{2}-2\;({\bmod {\;}}p)$

und schließlich

$2\equiv (2k-1)^{2}\;({\bmod {\;}}p)$

Damit ist (wieder unter Benutzung des Legendre-Symbols)

$\left({\frac {2}{p}}\right)=1$.

Daraus folgt mit zweitem Ergänzungssatz zum quadratischen Reziprozitätsgesetz

${\begin{aligned}1&=(-1)^{\frac {p^{2}-1}{8}}\\&=(-1)^{\frac {(p+1)(p-1)}{8}}\\&=(-1)^{\frac {(4\lambda +2)4\lambda }{8}}\\&=(-1)^{(2\lambda +1)\lambda }\\&=(-1)^{\lambda }\\\end{aligned}}$

Anmerkung

1. Ähnliche Folgerungen lassen sich auch für andere Kongruenzen ableiten.
2. Die Ausssagen A1c und A2b und A3b sind auch leicht direkt nachzurechnen.

Hilfslinks

1. Beweisarchiv
2. Design Resources on the Web

Literatur

• Thomas Beth - Dieter Jungnickel - Hanfried Lenz: Design Theory. Bibliographisches Institut, Mannheim / Wien / Zürich 1985, ISBN 3-411-01675-2. 
• Albrecht Beutelspacher: Einführung in die endliche Geometrie II. Projektive Räume. Bibliographisches Institut, Mannheim / Wien / Zürich 1983, ISBN 3-411-01648-5.  MR0670590
• Peter Bundschuh: Einführung in die Zahlentheorie. 2. Auflage. Springer-Verlag, Berlin [u.a.] 1992, ISBN 3-540-55178-6.  MR1260931
• P. J. Cameron - J. H. van Lint: Designs, Graphs, Codes and their Links (= London Mathematical Society Student Texts. Band 22). Cambridge University Press, Cambridge (u.a.) 1991, ISBN 0-521-42385-6. 
• Tosiro Tsuzuku: Finite Groups and Finite Geometries (= Cambridge Tracts in Mathematics. Band 78). Cambridge University Press, Cambridge (u. a.) 1982, ISBN 0-521-22242-7. 

Einzelnachweise und Fußnoten

K references />

KK Kategorie:Endliche Geometrie]] KK Kategorie:Blockplan]]

Überlegungen zur Unschärferelation von Heisenberg

1)

Ich bin mir da nicht sicher: Erstens meines eigenen Standpunkts nicht und zweitens in der Frage, ob ich überhaupt weiter Stellung nehmen sollte. Aber ich denke schlussendlich, ich sollte es tun - selbst wenn ich nun ziemlich spekulativ werden muss, was ich ansonsten nur ungern tue.

Also folgendes: In Hinblick auf die Unschärferelation sollten aus grundsätzlichen Erwägungen Zweifel bestehen, ob diese mit der gewöhnlichen Sprache überhaupt erfassbar ist. Zu dieser Schlussfolgerung wird man mE gedrängt, wenn man sich vor Augen hält, dass selbst unter den "Großvätern" der Quantenphysik ganz unterschiedliche Deutungsansätze im Zusammenhang mit der Unschärferelation und der Quantenmechanik vorgetragen wurden. So waren neben Albert Einstein und Erwin Schrödinger - wie ich bei Walter Greiner las - etwa auch Louis de Broglie und Max von Laue Gegner der Kopenhagener Deutung.

Auf der Suche nach einer Erklärung dafür habe ich mir zurecht gelegt, dass das Problem in der Sprache liegt. Die gewöhnliche Sprache ist einfach nicht tauglich , solch komplexe formale Zusammenhänge zu erfassen.

Die gewöhnliche Sprache orientiert sich am und erwächst aus dem Alltag des Menschen. Dagegen beziehen sich die Unschärferelation und die Quantenphysik insgesamt auf das Geschehen im Mikrokosmos. Das Geschehen im Mikrokosmos und das im menschlichen Alltag haben mE aber nichts gemein. Daher kann keine Erwartung bestehen, dass das Geschehen im Mikrokosmos und speziell die Unschärferelation mittels gewöhnlicher Sprache erfassbar seien. Nach Lage der Dinge scheint es eher so zu sein, dass die einzige "Sprache", mit der das Geschehen im Mikrokosmos erfassbar wird, die "Sprache der Mathematik" ist, dass man aber nicht erwarten kann, durch sie umfassend deutungsfähige Ergebnisse zu erzielen.

2)

Da ich diese Gegenrede begonnen habe, erlaube ich mir ein Schlusswort: Dann können wir gern - wie ja einige meiner Vorredner empfehlen - zum Ende der Diskussion kommen.

A) Meiner Spekulation über das Verhältnis der gewöhnlichen Sprache des Alltags zum Mikrokosmos braucht man nicht zu folgen.

B) Wichtig ist mir die obige erste Feststellung, die - auch wegen meiner Spekulation , wie ich eingestehe - zu sehr in den Hintergrund gerückt ist und die ich hier noch einmal verdeutlichen möchte:

Für die gesamte moderne Physik sind die Mathematik und der mathematische Formalismus unverzichtbar.

C) Konkret bezogen auf die Quantenmechanik insgesamt und auf die Heisenbergsche Unschärferelation im Besonderen meine ich sogar:

Sie sind undenkbar ohne die Fortschritte auf dem Gebiet der Analysis und der Funktionalanalysis und inbesondere auf dem Gebiet der Hilbertraum- und der Operatorentheorie.

Mehr noch: Beides ist aufs Engste miteinander verknüpft und tatsächlich muss von einer gegenseitigen Befruchtung gesprochen werden. Denn auch die stürmische Entwicklung der Analysis und der Funktionalanalysis im 20. Jh. fand nicht zuletzt wegen der Problemstellungen seitens der Quantenmechanik statt. Zu dieser Sichweise sieht man schon deswegen sich gedrängt, weil zu bemerken ist, dass sich daran einige der bedeutendsten Mathematiker dieser Zeit wie David Hilbert, Hermann Weyl und John von Neumann beteiligt haben.

Weitergehende Überlegungen

Einleitung

Die heisenbergsche Unschärferelation bringt zwei Messgrößen $A\;,\;B$ eines quantenmechanischen Systems miteinander in Beziehung und wird dahingehend interpretiert, dass es unmöglich sei, beide gleichzeitig mit beliebiger Genauigkeit zu bestimmen:

Je genauer man $A$ bestimmt, desto ungenauer fällt die Bestimmung von $B$ aus und vice versa.

Auf der anderen Seite steht die heisenbergsche Vertauschungsrelation, wonach die zugeordneten selbstadjungierten Operatoren ${\hat {A}}\;,\;{\hat {B}}$ die folgende Gleichung erfüllen:

$[{\hat {A}},{\hat {B}}]={\frac {h}{2\pi \mathrm {i} }}\mathbf {1} _{\mathcal {H}}$

Das heißt:

Es soll für jeden Zustandsvektor $\psi$ stets die Gleichung

$\langle \mathrm {i} \cdot ({\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}})\psi ,\psi \rangle ={\frac {h}{2\pi }}\cdot {\|\psi \|}^{2}$

gelten.

Das bedeutet:

Es wird für zwei Messgrößen, die man zu keinem Zeitpunkt gleichzeitig exakt bestimmen kann, dennoch gesagt, dass als sicher gelten kann, dass die ihnen zugeordneten Operatoren für jeden Zustand des quantenmechanischen Systems die obige Gleichung exakt erfüllen. Darin scheint eine Widersprüchlichkeit zu liegen und es stellt sich die Frage, wie man dieser umgehen kann.

Eine Möglichkeit, dies zu tun, liegt darin, die Herleitung der Unschärferelation, wie sie durch John von Neumann geliefert wurde, dahingehend abzuwandeln, dass die Unschärferelation nicht unter Annahme der Vertauschungsrelation, sondern unter Annahme einer Abschwächung hergeleitet wird, welche die obige Widersprüchlichkeit nicht beinhaltet.

Man kann nämlich anstelle der Vertauschungsrelation voraussetzen, dass der Operator $\mathrm {i} \cdot [{\hat {A}},{\hat {B}}]$ stattdessen der Bedingung

$\mathrm {i} \cdot [{\hat {A}},{\hat {B}}]\geq {\frac {h}{2\pi }}\mathbf {1} _{\mathcal {H}}$

genügt.

Diese Bedingung kennt man in ähnlicher Form aus der Theorie der linearen Operatoren auf Hilberträumen und auch aus der Analysis und Funktionalanalysis bei den (nach unten) halbbeschränkten Operatoren.

Was diese abgeschwächte Bedingung besagt, lässt sich auch so darstellen:

Es soll für jedes $\psi$ des Definitionsbereichs dieses Operators (bei sonst gleichen Voraussetzungen) durchweg

(1) $\langle \mathrm {i} \cdot [{\hat {A}},{\hat {B}}]\psi ,\psi \rangle \in \mathbb {R}$

(2) $\langle \mathrm {i} \cdot [{\hat {A}},{\hat {B}}]\psi ,\psi \rangle \geq {\frac {h}{2\pi }}\cdot {\|\psi \|}^{2}$

als gegeben angenommen werden.

Der Beweis auf Basis dieser Voraussetzung verläuft analog dem bei v. Neumann. Nämlich wie folgt:

Exakte Herleitung auf Beweis auf Basis der abgeschwächten Bedingung

Als gegeben werden angenommen:

1) Ein Hilbertraum

${\mathcal {H}}$

mit dem Skalarprodukt

$\langle \cdot ,\cdot \rangle$

und der dazugehörigen Norm

$\|\cdot \|={\langle \cdot ,\cdot \rangle }^{\frac {1}{2}}$

und mit

$\mathbf {1} _{\mathcal {H}}$

als Identitätsoperator auf ${\mathcal {H}}$

sowie

2) Zwei in ${\mathcal {H}}$ definierte selbstadjungierte lineare Operatoren

${\hat {A}}\colon {\mathcal {H}}\supset D({\hat {A}})\to {\mathcal {H}}$

und

${\hat {B}}\colon {\mathcal {H}}\supset D({\hat {B}})\to {\mathcal {H}}$

mit der Eigenschaft

$\mathrm {i} \cdot [{\hat {A}},{\hat {B}}]\geq C\cdot \mathbf {1} _{\mathcal {H}}$ mit $C={\frac {h}{2\pi }}$

3) Ein

$\psi \in {\;{\bigl (}D({\hat {A}})\cap D({\hat {B}})\cap {\hat {A}}^{-1}(D({\hat {B}}))\cap {\hat {B}}^{-1}(D({\hat {A}})){\bigr )}\;}\subseteq {\mathcal {H}}$

der Norm

$\|\psi \|=1$

Davon ausgehend lassen sich die folgenden Rechenschritte durchführen:

Schritt 1

Es ist:

$\operatorname {Im} {\langle {\hat {A}}\psi ,{\hat {B}}\psi \rangle }={\frac {\langle {\hat {A}}\psi ,{\hat {B}}\psi \rangle -\langle {\hat {B}}\psi ,{\hat {A}}\psi \rangle }{2\mathrm {i} }}$

Also gilt:

$2\cdot \operatorname {Im} {\langle {\hat {A}}\psi ,{\hat {B}}\psi \rangle }=-{\mathrm {i} }\cdot (\langle {\hat {B}}{\hat {A}}\psi ,\psi \rangle -\langle {\hat {A}}{\hat {B}}\psi ,\psi \rangle )=-{\mathrm {i} }\cdot \langle {\hat {B}}{\hat {A}}\psi -{\hat {A}}{\hat {B}}\psi ,\psi \rangle$

$=\langle (\mathrm {i} \cdot ({\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}})\psi ),\psi \rangle =\langle (\mathrm {i} \cdot [{\hat {A}},{\hat {B}}])\psi ,\psi \rangle \geq C\cdot {\|\psi \|}^{2}$

Das bedeutet:

${\|\psi \|}^{2}\leq {\frac {2}{C}}\cdot \operatorname {Im} {\langle {\hat {A}}\psi ,{\hat {B}}\psi \rangle }\leq {\frac {2}{C}}\cdot |\langle {\hat {A}}\psi ,{\hat {B}}\psi \rangle |$

Also folgt mit der cauchy-schwarzschen Ungleichung:

${\|\psi \|}^{2}\leq {\frac {2}{C}}\cdot \|{\hat {A}}\psi \|\cdot \|{\hat {B}}\psi \|$

Schritt 2

Sind nun $r,s\in \mathbb {C}$ zwei beliebige Skalare, so gilt - wie man leicht nachrechnet - die oben angenommene Halbbeschränktheitsbedingung in gleicher Weise auch für ${\hat {A}}_{r}={\hat {A}}-r\mathbf {1} _{\mathcal {H}}$ und ${\hat {B}}_{s}={\hat {B}}-s\mathbf {1} _{\mathcal {H}}$.

Folglich hat man stets ganz allgemein:

${\|\psi \|}^{2}\leq {\frac {2}{C}}\cdot \|{\hat {A}}_{r}\psi \|\cdot \|{\hat {B}}_{s}\psi \|={\frac {2}{C}}\cdot \|{\hat {A}}\psi -r\psi \|\cdot \|{\hat {B}}\psi -s\psi \|$

Schritt 3

Infolge des Schrittes 2 erhält man für $\|\psi \|=1$, $r=\langle {\hat {A}}\psi ,\psi \rangle$ und $s=\langle {\hat {B}}\psi ,\psi \rangle$ stets

$\|{\hat {A}}\psi -\langle {\hat {A}}\psi ,\psi \rangle \psi \|\cdot \|{\hat {B}}\psi -\langle {\hat {B}}\psi ,\psi \rangle \psi \|\geq {\frac {C}{2}}\cdot$

Schritt 4

Wegen $C={\frac {h}{2\pi }}$ gewinnt man nun sofort die heisenbergsche Unschärferelation:

$\|{\hat {A}}\psi -\langle {\hat {A}}\psi ,\psi \rangle \psi \|\cdot \|{\hat {B}}\psi -\langle {\hat {B}}\psi ,\psi \rangle \psi \|\geq {\frac {h}{4\pi }}\cdot$

Benutzte Quellen

• Johann v. Neumann: Mathematische Grundlagen der Quantenmechanik. Unveränderter Nachdruck der 1. Auflage von 1932. Kapitel III „Die quantenmechanische Statistik.“ Abschnitt 4 „Unbestimmheitsrelationen“ (= Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. Band 38). Springer-Verlag, Berlin [u. a.] 1968, ISBN 3-540-04133-8, S. 123–124.  MR0223138
• Hans Triebel: Höhere Analysis (= Hochschulbücher für Mathematik. Band 76). 8., aktualisierte Auflage. VEB Deutscher Verlag der Wissenschaften, Berlin 1972. 

Fußnoten

K references />

π-Formeln der Funktionentheorie

Auch in der Funktionentheorie bzw. komplexen Analysis spielt die Kreiszahl eine wesentliche Roll. Hier ist an erster Stelle

• die Integralformel von Cauchy: $f(z)={\frac {1}{2\pi i}}\oint _{\gamma }{\frac {f(\zeta )}{\zeta -z}}\mathrm {d} \zeta .$

zu nennen.

Die Bedeutung der Kreiszahl wird darüber hinaus augenfällig in den Formeln zur Partialbruchzerlegung der komplexwertigen trigonometrischen Funktionen nach dem Satz von Mittag-Leffler . Hier sind insbesondere zu erwähnen

• die Partialbruchzerlegung des Kotangens:

$\pi \cot(\pi z)=z\cdot \sum _{n={-\infty }}^{+\infty }{\frac {1}{z^{2}-n^{2}}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\bigl (}{\frac {1}{z-n}}+{\frac {1}{z+n}}{\bigr )}={\frac {1}{z}}+2z\cdot \sum _{n=1}^{\infty }{\frac {1}{z^{2}-n^{2}}}\;\;(z\in {\mathbb {C} \setminus \mathbb {Z} })$

sowie die daraus - neben weiteren! - zu gewinnenden

• Partialbruchzerlegungen für Sinus und Kosinus:

${\bigl (}{\frac {\pi }{\sin(\pi z)}}{\bigr )}^{2}=\sum _{n={-\infty }}^{+\infty }{\frac {1}{(z-n)^{2}}}\;\;(z\in {\mathbb {C} \setminus \mathbb {Z} })$

${\bigl (}{\frac {\pi }{\cos(\pi z)}}{\bigr )}^{2}=\sum _{n={-\infty }}^{+\infty }{\frac {1}{(z-{\tfrac {2n-1}{2}})^{2}}}\;\;(z\in {\mathbb {C} \setminus \{{\frac {2n-1}{2}}\colon n\in \mathbb {Z} \}})$   .

Die genannte Partialbruchzerlegung für den Sinus liefert dann durch Einsetzen von $z={\frac {1}{2}}$ die bekannten Reihendarstellung:

${\frac {{\pi }^{2}}{8}}=1+{\frac {1}{9}}+{\frac {1}{25}}+{\frac {1}{49}}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{2}}}$   ,

welche ihrerseits direkt zu der eulerschen Reihendarstellung

${\frac {{\pi }^{2}}{6}}=1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+\cdots =\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}$

führt.

Quellen

• Heinrich Behnke - Friedrich Sommer: Theorie der analytischen Funktionen einer komplexen Veränderlichen (= DIE GRUNDLEHREN DER MATHEMATISCHEN WISSENSCHAFTEN IN EINZELDARSTELLUNGEN. Band 77). Springer-Verlag, Berlin - Heidelberg - New York 1965. 
• Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications. Band 94). Cambridge Univity Press, Cambridge (u. a.) 2003, ISBN 0-521-81805-2.  MR2003519.

• Klaus Jänich: Einführung in die Funktionentheorie. 2. Auflage. Springer-Verlag, Berlin (u. a.) 1980, ISBN 3-540-10032-6.  MR0636508
• Konrad Knopp: Theorie und Anwendung der unendlichen Reihen (= Die Grundlehren der Mathematischen Wissenschaften. Band 2). 5., berichtigte Auflage. Springer Verlag, Berlin - Göttingen - Heidelberg - New York 1964, ISBN 3-540-03138-3.  MR0183997
• Konrad Knopp: Funktionentheorie II. Anwendungen und Weiterführung der allgemeinen Theorie (= Sammlung Göschen. Band 703). 11. Auflage. de Gruyter, Berlin 1965. 

Zur heronschen Formel

Der Satz des Heron ist ein Lehrsatz der Elementargeometrie, welcher nach dem antiken Mathematiker Heron von Alexandria benannt ist. Der Satz beschreibt eine mathematische Formel, mit deren Hilfe der Flächeninhalt eines Dreiecks aus den drei Seitenlängen berechenbar ist. Man nennt die Formel auch heronsche Formel bzw. heronische Formel oder auch die Formel von Heron (englisch Heron's_formula).

Formulierung des Satzes

Der Flächeninhalt $F_{\Delta }$ eines Dreiecks $\Delta$ der euklidischen Ebene mit den Seitenlängen

$a,b,c$

und halbem Umfang

$s\,=\,{\frac {a+b+c}{2}}$

ist

$F_{\Delta }={\sqrt {s(s-a)(s-b)(s-c)}}$   .

Umrechnungen

Die heronische Formel lässt sich auch so ausdrücken:

(V1) $F_{\Delta }={\frac {\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}{4}}$   .

Ausmultipliziert erhält man:

(V2) $F_{\Delta }={\frac {\sqrt {2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}-a^{4}-b^{4}-c^{4}}}{4}}$   .

Als andere Darstellung der heronischen Formel ist auch folgende gängig:

(V3) $F_{\Delta }={\frac {\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}{4}}$   ,

welche man aus der Version (V1) durch Umgruppieren und Anwendung der binomischen Formeln mit den folgenden Gleichungen gewinnt:

${\begin{aligned}16{F_{\Delta }}^{2}&={\bigl (}((a+b)+c)((a+b)-c){\bigr )}{\bigl (}(c+(a-b))(c-(a-b)){\bigr )}\\&={\bigl (}(a+b)^{2}-c^{2}{\bigr )}{\bigl (}c^{2}-(a-b)^{2}{\bigr )}\\&={\bigl (}a^{2}+2ab+b^{2}-c^{2}{\bigr )}{\bigl (}c^{2}-a^{2}+2ab-b^{2}{\bigr )}\\&={\bigl (}2ab+(a^{2}+b^{2}-c^{2}){\bigr )}{\bigl (}2ab-(a^{2}+b^{2}-c^{2}){\bigr )}\\&=4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}\\\end{aligned}}$   .

Aus der Version (V3) schließlich lässt sich die folgende Determinantendarstellung ableiten:

(V4) $F_{\Delta }={\frac {1}{4}}{\sqrt {-\det \left({\begin{matrix}0&1&1&1\\1&0&a^{2}&b^{2}\\1&a^{2}&0&c^{2}\\1&b^{2}&c^{2}&0\end{matrix}}\right)}}$   .

Denn man erhält mittels elementarer Matrizenumformungen und unter Anwendung des Entwicklungssatzes von Laplace folgende Gleichungen:

${\begin{aligned}4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}&=4a^{2}b^{2}-(c^{2}-a^{2}-b^{2})^{2}\\&=\det \left({\begin{matrix}-2a^{2}&c^{2}-a^{2}-b^{2}\\c^{2}-a^{2}-b^{2}&-2b^{2}\end{matrix}}\right)\\&=\det \left({\begin{matrix}1&a^{2}&b^{2}\\0&-2a^{2}&c^{2}-a^{2}-b^{2}\\0&c^{2}-a^{2}-b^{2}&-2b^{2}\end{matrix}}\right)\\&=\det \left({\begin{matrix}1&a^{2}&b^{2}\\1&-a^{2}&c^{2}-a^{2}\\1&c^{2}-b^{2}&-b^{2}\end{matrix}}\right)\\&=-\det \left({\begin{matrix}0&1&0&0\\1&0&a^{2}&b^{2}\\1&a^{2}&-a^{2}&c^{2}-a^{2}\\1&b^{2}&c^{2}-b^{2}&-b^{2}\end{matrix}}\right)\\&=-\det \left({\begin{matrix}0&1&1&1\\1&0&a^{2}&b^{2}\\1&a^{2}&0&c^{2}\\1&b^{2}&c^{2}&0\end{matrix}}\right)\\\end{aligned}}$   .

Weiterer Zusammenhang

Die heronische Formel kann als Grenzfall aus der Formel für den Flächeninhalt $F_{\Sigma }$ eines Sehnenvierecks $\Sigma$ gewonnen werden, wenn zwei der Eckpunkte ineinander übergehen, so dass eine der Seiten des Sehnenvierecks die Länge Null annimmt. Für den Flächeninhalt eines Sehnenvierecks gilt nämlich nach der Formel von Brahmagupta

$F_{\Sigma }={\sqrt {(s-a)(s-b)(s-c)(s-d)}}$   ,

wobei hier der halbe Umfang

$s\,=\,{\frac {a+b+c+d}{2}}$

ist.

Anmerkungen

1. Für die Herleitung der heronischen Formel gibt es viele Vorgehensweisen. Insbesondere lässt sie sich elementar mit Hilfe des pythagoreischen Lehrsatzes herleiten.
2. Neben der Zuweisung der Formel an Heron von Alexandria gibt es auch eine Zuweisung, derzufolge sie auf Archimedes zurückgeht.

Weblinks

• Eric W. Weisstein: Satz des Heron. In: MathWorld (englisch).
• Elementarer Beweis
• Beweis mit Hilfe des Kosinussatzes (Deutsch) (PDF-Datei; 88 kB)
• Beweis für den Satz des Heron und seine Folgerungen (PDF-Datei; 82 kB)

Beweis der heronschen Formel mit dem Satz des Pythagoras

Der Beweis geht etwa wie folgt:

In einem gegebenen Dreieck $\triangle ABC$, von dem man oBdA annehmen kann, dass für die Seitenlängen $a=|BC|$, $b=|CB|$ und $c=|AB|$ die Ungleichungen $b\leq a\leq c$ gelten, sei $D$ der Fußpunkt der Höhe vom Eckpunkt $C$ auf die Seite $AB$ . Weiter sei $q=|AD|$ und $p=|DB|$ und damit $p+q=c$.

Nach dem pythagoreischen Lehrsatz gelten dann die beiden folgenden Identitäten:

$h^{2}+p^{2}=a^{2}$

$h^{2}+q^{2}=b^{2}$

Daraus folgt

$b^{2}-a^{2}=q^{2}-p^{2}=(q+p)(q-p)=c(q-p)$

und weiter

${\frac {b^{2}-a^{2}}{c}}=q-p=c-2p$

und daraus

$p={\frac {a^{2}-b^{2}+c^{2}}{2c}}$   .

Dies ergibt

$h^{2}=a^{2}-p^{2}=a^{2}-{\bigl (}{\frac {a^{2}-b^{2}+c^{2}}{2c}}{\bigr )}^{2}$   .

Hinsichtlich der Dreiecksfläche $F$ bedeutet dies

${\begin{aligned}16F^{2}&=4h^{2}c^{2}\\&=4a^{2}c^{2}-{\bigl (}a^{2}-b^{2}+c^{2}{\bigr )}^{2}\\&={\bigl (}2ac+a^{2}-b^{2}+c^{2}{\bigr )}{\bigl (}2ac-a^{2}+b^{2}-c^{2}{\bigr )}\\&={\bigl (}(a+c)^{2}-b^{2}{\bigr )}{\bigl (}b^{2}-(a-c)^{2}{\bigr )}\\&=(a+c+b)(a+c-b)(b+a-c)(b-a+c)\\&=2s(2s-2b)(2s-2c)(2s-2a)\\\end{aligned}}$

Also gilt insgesamt

$F={\sqrt {s(s-a)(s-b)(s-c)}}$   .

Folgerung der heronschen Formel aus dem Schenkeltransversalensatz nach Dörrie

Heinrich Dörrie zeigt, hat der Schenkeltransversalensatz eine Anzahl von interessanten Folgerungen. So impliziert er beispielweise die berühmte Formel von Heron. Diese Herleitung lässt sich wiedergeben wie folgt:

Schritt I

In einem gegebenen Dreieck $\triangle ABC$, von dem man oBdA annehmen kann, dass für die Seitenlängen $a=|BC|$, $b=|CB|$ und $c=|AB|$ die Ungleichungen $b\leq a\leq c$ gelten, spiegelt man den Eckpunkt $B$ an der Höhe von $C$ auf die Seite $AB$ und erhält den Spiegelpunkt $B^{'}$. (Dabei ist für den Fall, dass $\triangle ABC$ gleichschenklig ist, $A=B^{'}$. )

Mit der Setzung:

$x=|AB^{'}|$.

folgt wegen der nach Konstruktion gegebenen Gleichschenkligkeit von $\triangle B^{'}BC$ zunächst :

${\tfrac {c+x}{2}}=|B^{'}B|$

Wegen:

$a=|CB^{'}|$

ergibt sich dann gemäß der 2. Variante des Schenkeltransversalensatzes, angewandt auf $\triangle B^{'}BC$:

$b^{2}=a^{2}-xc$

und daraus sofort:

$xc=a^{2}-b^{2}$

Schritt II

Wiederum gemäß der 2. Variante des Schenkeltransversalensatzes (oder auch nach dem Satz des Pythagoras, welcher ja wie erwähnt als Folge des Schenkeltransversalensatzes betrachtet werden kann) und wenn wie üblich die Länge der Höhe von $C$ auf die Seite $AB$ mit $h$ bezeichnet wird, ergibt sich dann weiter:

$h^{2}=a^{2}-{\tfrac {c+x}{2}}\cdot {\tfrac {c+x}{2}}=a^{2}-{\tfrac {(c+x)^{2}}{4}}$

und dann:

$4h^{2}=4a^{2}-(c+x)^{2}=(2a+(c+x))\cdot (2a-(c+x))=(2a+c+x)\cdot (2a-c-x)$

Für den Flächeninhalt $F_{ABC}={\tfrac {h\cdot c}{2}}$ ergibt sich damit:

$16{F_{ABC}}^{2}=4h^{2}c^{2}=(2ac+c^{2}+xc)\cdot (2ac-c^{2}-xc)$

Schritt III

Schritt I und Schritt II zusammen führen auf die Gleichung:

$16{F_{ABC}}^{2}=(2ac+c^{2}+a^{2}-b^{2})^{(}2ac-c^{2}-a^{2}+b^{2})=((a+c)^{2}-b^{2})\cdot (b^{2}-(a-c)^{2})=(a+c+b)\cdot (a+c-b)\cdot (b+a-c)\cdot (b-a+c)$

Mit der üblichen Setzung:

$s={\tfrac {a+b+c}{2}}$

und nach Vertauschung der Klammern hat man dann:

$16{F_{ABC}}^{2}=2s\cdot (2s-2a)\cdot (2s-2b)\cdot (2s-2c)$

und weiter:

${F_{ABC}}^{2}=s\cdot (s-a)\cdot (s-b)\cdot (s-c)$

und schließlich:

${F_{ABC}}={\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}}$

Aus der der heronschen Formel folgt der Satz des Pythagoras

Einerseits gilt für den Flächeninhalt

$A={\frac {ab}{2}}$

und anderseits nach Heron

$A={\sqrt {s(s-a)(s-b)(s-c)}}$

mit

$s={\frac {a+b+c}{2}}$   .

Also folgt nacheinander und unter Benutzung der binomischen Formeln

${\frac {a^{2}b^{2}}{4}}=s(s-a)(s-b)(s-c)$

und daraus

${\begin{aligned}4a^{2}b^{2}&=(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\\&={\bigl (}-a^{2}+(b+c)^{2}{\bigr )}{\bigl (}a^{2}-(b-c)^{2}{\bigr )}\\&=-a^{4}+a^{2}{\bigl (}(b+c)^{2}+(b-c)^{2}{\bigr )}-{\bigl (}b^{2}-c^{2}{\bigr )}^{2}\\&=-a^{4}+a^{2}{\bigl (}2b^{2}+2c^{2}{\bigr )}-{\bigl (}b^{4}-2b^{2}c^{2}+c^{4}{\bigr )}\\&=-a^{4}+2a^{2}b^{2}+2a^{2}c^{2}-b^{4}+2b^{2}c^{2}-c^{4}\\\end{aligned}}$

und daraus

$a^{4}+b^{4}+c^{4}+2a^{2}b^{2}-2a^{2}c^{2}-2b^{2}c^{2}=0$

und schließlich

${\bigl (}a^{2}+b^{2}-c^{2}{\bigr )}^{2}=0$

Folglich ist

$a^{2}+b^{2}=c^{2}$  .

Literatur

• Heinrich Dörrie: Der Schenkel-Transversalensatz, Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht 53, 1922, S. 8–14 (Jahrbuch-Rezension)
• A. M. Fraedrich: Die Satzgruppe des Pythagoras (= Lehrbücher und Monographien zur Didaktik der Mathematik. Band 29). B.I.-Wissenschaftsverlag, Mannheim - Leipzig - Wien - Zürich 1994, ISBN 3-411-17321-1. 
• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 2. 13. Auflage. Ernst Klett Verlag, Stuttgart 1965. 
• Hermann Athen, Jörn Bruhn (Hrsg.): Lexikon der Schulmathematik und angrenzender Gebiete. Band 2: F–K. Aulis Verlag Deubner & CO KG, Köln 1977, ISBN 3-7614-0242-2. 
• A. M. Fraedrich: Die Satzgruppe des Pythagoras (= Lehrbücher und Monographien zur Didaktik der Mathematik. Band 29). B.I.-Wissenschaftsverlag, Mannheim - Leipzig - Wien - Zürich 1994, ISBN 3-411-17321-1. 
• György Hajós: Einführung in die Geometrie. (BEVEZETÉS A GEOMETRIÁBA. Deutsche Übersetzung und Redaktion: DR. G. EISENREICH (Leipzig)). B. G. Teubner Verlag, Leipzig 1970. 
• Max Koecher, Aloys Krieg: Ebene Geometrie. 3., neu bearbeitete und erweiterte Auflage. Springer Verlag, Berlin (u. a.) 2007, ISBN 978-3-540-49327-3. 
• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 2. 13. Auflage. Ernst Klett Verlag, Stuttgart 1965. 

Schenkeltransversalensatz (Ursprüngliche Version von mir)

Der Schenkeltransversalensatz ist ein Satz der Elementargeometrie der Dreiecke, welcher mit dem Satz des Pythagoras gleichwertig ist.

Formulierung des Satzes

Gegeben sei ein gleichschenkliges Dreieck $\Delta =ABC$ mit Basiswinkeln bei den Eckpunkten $A$ und $B$ und der Spitze im Eckpunkt $C$. Die durch die Basis von $\Delta$ verlaufende Gerade sei $g=AB$.

Weiter sei gegeben eine Transversale durch die Spitze $C$ von $\Delta$, welche $g$ in einem Punkt $P$ schneidet.

Dann gilt:

(*) ${\overline {CP}}^{2}={\overline {AC}}^{2}+\epsilon \cdot {\overline {PA}}\cdot {\overline {PB}}$

mit:

$\epsilon =-1$, falls $P$ zwischen $A$ und $B$ liegt

$\epsilon =+1$ sonst

Beweis des Satzes

Man darf ohne oBdA annehmen, dass das Dreieck $\Delta =ABC$ eine geometrische Figur der komplexen Zahlenebene darstellt. Dabei lassen sich sogar folgende Gegebenheiten annehmen:

1. Die Gerade $g$ fällt mit der reellen Achse $\mathbb {R} \subset \mathbb {C}$ zusammen.
2. Die Spitze $C$ liegt auf der imaginären Achse.
3. Der Höhenfußpunkt der von $C$ auf $g$ gefällten Höhe fällt mit $0$ zusammen.
4. Es ist $A<0<B$

Denn folgt der Satz für diesen speziellen Fall, so folgt er allgemein, da die Geometrie der komplexen Zahlenebene mit der ebenen euklidischen Geometrie übereinstimmt und da zu einem gegebenen rechtwinkligen Dreieck durch Anwendung geeignet gewählter ebene Kongruenzabbildungen stets ein spezielles Dreieck der genannten Art, welches zu jenem kongruent ist, gefunden werden kann.

Erste Folgerungen

Es ist $[A,B]\subset \mathbb {R}$ mit $A=-B$.

Weiter ist $P\in \mathbb {R}$ und $C\in {\mathrm {i} }\mathbb {R}$.

Fallunterscheidung

Drei Fälle sind zu betrachten:

(I) : $P<A$

Dann gilt:

$\epsilon =+1$

und weiter:

$\epsilon \cdot {\overline {PA}}\cdot {\overline {PB}}=|P-A|\cdot |P-B|=(A-P)\cdot (B-P)=(A-P)\cdot (-A-P)=-(A-P)\cdot (A+P)=P^{2}-A^{2}$

(II) : $A\leq P\leq B$

Dann gilt:

$\epsilon =-1$

und weiter:

$\epsilon \cdot {\overline {PA}}\cdot {\overline {PB}}=-(P-A)\cdot (B-P)=(P-A)\cdot (-B+P)=(P-A)\cdot (A+P)=P^{2}-A^{2}$

(III) : $B<P$

Dann gilt:

$\epsilon =+1$

und weiter:

$\epsilon \cdot {\overline {PA}}\cdot {\overline {PB}}=(P-A)\cdot (P-B)=(P-A)\cdot (P+A)=P^{2}-A^{2}$

Schlussfolgerung

In jedem der drei obigen Fälle gewinnt man unter Anwendung des Pythagoreischen Lehrsatzes bzgl. der beiden rechtwinkligen Dreiecke $ADC$ und $PDC$ die folgenden Gleichungen:

${\overline {CP}}^{2}=|C|^{2}+P^{2}=(|C|^{2}+A^{2})+(P^{2}-A^{2})={\overline {AC}}^{2}+\epsilon \cdot {\overline {PA}}\cdot {\overline {PB}}$

und damit (*).

Gleichwertigkeit mit dem Pythagoreischen Lehrsatz

Der Schenkeltransversalensatz ergibt sich wie gesehen unter Anwendung des Pythagoreischen Lehrsatzes.

Andererseits impliziert der Schenkeltransversalensatz seinerseits den Pythagoreischen Lehrsatz. Diesen erhält man, indem man zu einem vorgegebenen rechtwinkligen Dreieck $ADC$ mit rechtem Winkel bei $D$ den Punkt $B$ als Spiegelpunkt von $A$ auf der Geraden $g=AD$ durch Punktspiegelung am Punkte $D$ konstruiert und zugleich $P=D$ setzt.

Dann ergibt sich gemäß Fall (II) oben:

${\overline {CD}}^{2}={\overline {CP}}^{2}={\overline {AC}}^{2}-{\overline {PA}}\cdot {\overline {PB}}={\overline {AC}}^{2}-{\overline {PA}}^{2}={\overline {AC}}^{2}-{\overline {AD}}^{2}$

und dann:

${\overline {CD}}^{2}+{\overline {AD}}^{2}={\overline {AC}}^{2}$.

Literatur

• Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 2. 13. Auflage. Ernst Klett Verlag, Stuttgart 1965. 
• Helmut Karzel, Hans-Joachim Kroll: Geschichte der Geometrie seit Hilbert. Wissenschaftliche Buchgesellschaft, Darmstadt 1988, ISBN 3-534-08524-8. 

Über den weierstraßschen Satz vom Maximum und Minimum

Dieser klassische Satz für stetige reellwertige Funktionen auf Kompakta wird in Topologie und Analysis auf die Tatsache zurückgeführt - vgl. etwa Schubert, S. 62, und Forster, S. 32 - dass das stetige Bild eines Kompaktums stets eine kompakte Teilmenge der reellen Zahlen , also nach dem Satz von Heine-Borel-Lebesgue immer abgeschlossen und beschränkt innerhalb $\mathbb {R}$ ist und dass damit die Bildmenge einer stetigen reellwertigen Funktion zwingend ihr Supremum und genauso ihr Infimum enthalten muss.

Diese Argumentation stellt die Hausdorffeigenschaft, also die Separiertheit von $\mathbb {R}$ in Rechnung, denn aus dieser folgt, dass kompakte Teilmengen von $\mathbb {R}$ notwendig abgeschlossen sind.

Der weierstraßschen Satz lässt sich jedoch unabhängig von allen Separiertheitsbetrachtungen mit Hilfe eines einfachen Widerspruchsbeweises beweisen, wobei sich zeigt, dass dabei die Hausdorffeigenschaft von $\mathbb {R}$ ohne Belang ist und dass auch die meisten der anderen charakteristischen Eigenschaften von $\mathbb {R}$ (wie etwa die Vollständigkeit) zum Beweis nicht benötigt werden.

Vielmehr zeigt sich, dass der weierstraßschen Satz im Wesentlichen aus ordnungstheoretischen und logischen Gründen gilt. Dies ergibt sich aus der folgenden allgemeinen Proposition (Proposition über Maximalstellen), welche sogar allgemeiner oberhalbstetige Abbildung einbezieht.

Proposition über Maximalstellen

Sie lässt sich formulieren wie folgt:

Gegeben seien nichtleere topologische Räume $(X,{\mathcal {O}}_{X})$ und $(Y,{\mathcal {O}}_{Y})$ mit Topologien ${\mathcal {O}}_{X}$ bzw. ${\mathcal {O}}_{Y}$.

$(X,{\mathcal {O}}_{X})$ sei quasikompakt.

Zudem sei $(Y,<)$ eine strikt geordnete Menge und die Ordnungsrelation $<$ sei mit der Topologie ${\mathcal {O}}_{Y}$ verträglich - in dem Sinne, dass alle Ordnungsideale der Gestalt $]\;,y_{0}[=\{y\in Y|y<y_{0}\}$   $(y_{0}\in Y)$ offen in $(Y,{\mathcal {O}}_{Y})$ sein sollen.

Weiter sei $f:(X,{\mathcal {O}}_{X})\to (Y,{\mathcal {O}}_{Y},<)$ eine oberhalbstetige Abbildung.

Dann gilt:

(B) Die Bildmenge $f(X)$ hat in der Relativordnung $<_{{\upharpoonright }{f(X)}}$ stets ein maximales Element.

Duale Proposition über Minimalstellen

In dualer Weise gilt:

Gegeben seien nichtleere topologische Räume $(X,{\mathcal {O}}_{X})$ und $(Y,{\mathcal {O}}_{Y})$ mit Topologien ${\mathcal {O}}_{X}$ bzw. ${\mathcal {O}}_{Y}$.

$(X,{\mathcal {O}}_{X})$ sei quasikompakt.

Zudem sei $(Y,<)$ eine strikt geordnete Menge und die Ordnungsrelation $<$ sei mit der Topologie ${\mathcal {O}}_{Y}$ im dualen Sinne verträglich, also so , dass alle Ordnungsfilter der Gestalt $]y_{0}\;,[=\{y\in Y|y>y_{0}\}$   $(y_{0}\in Y)$ offen in $(Y,{\mathcal {O}}_{Y})$ sein sollen.

Weiter sei $f:(X,{\mathcal {O}}_{X})\to (Y,{\mathcal {O}}_{Y},<)$ eine unterhalbstetige Abbildung.

Dann gilt:

(B) Die Bildmenge $f(X)$ hat in der Relativordnung $<_{{\upharpoonright }{f(X)}}$ stets ein minimales Element.

Beweis der Propositionen

Es ist aus Dualitätsgründen ausreichend, von den beiden Propositionen die erstere für den Fall der Maximalstellen von oberhalbstetigen Abbildungen zu beweisen.

Dazu wird die folgendes Annahme (A) zum Widerspruch geführt:

(A) Die Bildmenge $f(X)$ hat bezüglich $<_{{\upharpoonright }{f(X)}}$ kein maximales Element .

Aus (A) ergibt sich dann die folgende Identität :

(I) $X=\bigcup _{x\in X}{f^{-1}(]\;,f(x)[)}$   .

Denn (A) ist gleichbedeutend damit, dass für ein beliebiges $x_{0}\in X$ stets ein $x_{1}\in X$ derart existiert, dass $f(x_{0})<f(x_{1})$ erfüllt ist und damit auch $f(x_{0})\in \;]\;,f(x_{1})[$ und schließlich $x_{0}\in \;f^{-1}(]\;,f(x_{1})[)$   .

Nun ist weiter zu berücksichtigen, dass die vorausgesetzte Oberhalbstetigkeit von $f$ bedeutet, dass die Mengen in der Vereinigungsmenge auf der rechten Seite von (I) durchweg offen in $(X,{\mathcal {O}}_{X})$ sind.

In Verbindung mit der Quasikompaktheit von $(X,{\mathcal {O}}_{X})$ ergibt sich dann mit der Borel-Lebesgueschen Überdeckungseigenschaft, dass sogar schon für eine nichtleere endliche Teilmenge $A\subseteq X$

(II) $X=\bigcup _{a\in A}{f^{-1}(]\;,f(a)[)}$

gültig ist.

Da nun $(f(A),<_{{\upharpoonright }{f(A)}})$ eine endliche geordnete Menge und ebenfalls nichtleer ist, muss darin ein maximales Element, etwa

$f(a_{max})$ für ein $a_{max}\in A$

existieren.

Wegen (II) gibt es jedoch ein $a_{0}\in A$ mit

$a_{max}\in \;{f^{-1}(]\;,f(a_{0})[)}$  .

Das aber bedeutet

$f(a_{max})\in \;]\;,f(a_{0})[$

und daher

$f(a_{max})<f(a_{0})$  .

Letztere Ungleichung ist jedoch mit der Maximalität von $f(a_{max})$ in $(f(A),<_{{\upharpoonright }{f(A)}})$ unvereinbar.

Folglich kann (A) nicht gelten und statt dessen muss (B) wahr sein.

Korollar: Der Satz vom Maximum und Minimum

Dieser Satz folgt aus den obigen Propositionen aufgrund dessen, dass einerseits eine stetige reelle Funktion immer gleichzeitig oberhalb- und unterhalbstetig ist und dass andererseits $\mathbb {R}$ linear geordnet ist.

Es gilt demnach:

Für jeden quasikompakten topologischen Raum $(X,{\mathcal {O}}_{X})$und jede stetige reelle Funktion $f:(X,{\mathcal {O}}_{X})\to \mathbb {R}$ werden auf der Bildmenge $f(X)$ in der von den reellen Zahlen induzierten Relativordnung $<_{{\upharpoonright }{f(X)}}$ stets Maximum und Minimum angenommen.

Historie und Gewichtung des Resultats

Gemäß einem Papier von S. P. Franklin aus dem Jahre 1965 treten die beiden obigen Propositionen auch schon in der 1948er Ausgabe der Lattice Theory des amerikanischen Mathematikers Garrett Birkhoff auf. Franklin spricht hier vom theorem of Birkhoff. Wie Franklin zeigt, können die Aussagen beider Propositionen als charakteristisch für quasikompakte Räume betrachtet werden.

Zum Hintergrund: Ein allgemeiner Satz

Oben implizit mitbeweisen wurde der folgende allgemeine Satz:

Gegeben seien nichtleere topologische Räume $(X,{\mathcal {O}}_{X})$ und $(Y,{\mathcal {O}}_{Y})$ mit Topologien ${\mathcal {O}}_{X}$ bzw. ${\mathcal {O}}_{Y}$.

Zudem sei $(Y,<)$ eine strikt geordnete Menge und die Ordnungsrelation $<$ sei mit der Topologie ${\mathcal {O}}_{Y}$ verträglich.

Weiter sei $f:(X,{\mathcal {O}}_{X})\to (Y,{\mathcal {O}}_{Y},<)$ eine oberhalbstetige Abbildung.

Dann gilt:

Ist $T\subseteq X$ und hat dabei $X$ die Darstellung

$X=\bigcup _{t\in T}{f^{-1}(]\;,f(t)[)}$

so sind die Bildmenge $f(T)$ und damit auch $T$ und $X$ unendliche Mengen.

Hintergrundliteratur

• Otto Forster: Analysis 2 (= Grundkurs Mathematik). 8., aktualisierte Auflage. Vieweg+Teubner, Wiesbaden 2008, ISBN 978-3-8348-9541-7. 
• Bernhard Ganter: Diskrete Mathematik: Geordnete Mengen (= Springer-Lehrbuch). Springer Spektrum, Berlin - Heidelberg 2013, ISBN 978-3-642-37499-9. 
• Egbert Harzheim: Ordered Sets (= Advances in Mathematics. Band 7). Springer Verlag, New York, NY 2005, ISBN 0-387-24219-8.  MR2127991
• Horst Schubert: Topologie. Eine Einführung (= Mathematische Leitfäden). 4. Auflage. B. G. Teubner Verlag, Stuttgart 1975, ISBN 3-519-12200-6. 
• S. P. Franklin: Compactness and semi-continuity. In: Israel Journal of Mathematics. Band 3, 1965, S. 13–14 ([3] [PDF]).  MR0184195