Laplace-Verteilung
Die Laplace-Verteilung (benannt nach Pierre-Simon Laplace, einem französischen Mathematiker und Astronomen) ist eine stetige Wahrscheinlichkeitsverteilung. Da sie die Form zweier aneinandergefügter Exponentialverteilungen hat, wird sie auch als Doppelexponentialverteilung oder zweiseitige Exponentialverteilung[1] bezeichnet.
Definition
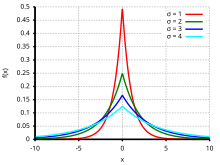
BearbeitenEine stetige Zufallsgröße unterliegt der Laplace-Verteilung mit dem Lageparameter und dem Skalenparameter , wenn sie die Wahrscheinlichkeitsdichte
besitzt.
Ihre Verteilungsfunktion lautet
Mittels der Signum-Funktion lässt sie sich geschlossen darstellen als
- .
Eigenschaften
BearbeitenSymmetrie
BearbeitenDie Wahrscheinlichkeitsdichte ist achsensymmetrisch zur Geraden und die Verteilungsfunktion ist punktsymmetrisch zum Punkt .
Erwartungswert, Median, Modalwert
BearbeitenDer Parameter ist gleichzeitig Erwartungswert, Median und Modalwert.
Varianz
BearbeitenDie Varianz wird durch den Parameter bestimmt.
Schiefe
BearbeitenDie Schiefe der Laplace-Verteilung ist
- .
Kurtosis
BearbeitenDie Wölbung einer Laplace-Verteilung ist identisch 6 (entspricht einem Exzess von 3).
Kumulanten
BearbeitenAlle Kumulante mit ungeradem Grad sind gleich Null. Für gerade gilt
Momenterzeugende Funktion
BearbeitenDie momenterzeugende Funktion eine Laplace-verteilten Zufallsgröße mit Parametern und lautet
- , für
Charakteristische Funktion
BearbeitenDie charakteristische Funktion entsteht aus der momenterzeugenden Funktion, indem man das Argument durch ersetzt, man erhält:
- .
Entropie
BearbeitenDie Entropie der Laplace-Verteilung (ausgedrückt in nats) beträgt
- .
Zufallszahlen
BearbeitenZur Erzeugung doppelexponentialverteilter Zufallszahlen bietet sich die Inversionsmethode an.
Die nach dem Simulationslemma zu bildende Pseudoinverse der Verteilungsfunktion lautet hierbei
- .
Zu einer Folge von Standardzufallszahlen lässt sich daher eine Folge
doppelexponentialverteilter Zufallszahlen berechnen.
Beziehung zu anderen Verteilungen
BearbeitenBeziehung zur Normalverteilung
BearbeitenSind unabhängige standardnormalverteilte Zufallsgrößen, dann ist standardlaplaceverteilt ( ).
Beziehung zur Exponentialverteilung
BearbeitenEine Zufallsvariable , die als Differenz zweier unabhängiger exponentialverteilter Zufallsvariablen und mit demselben Parameter definiert ist, ist Laplace-verteilt.[2]
Beziehung zur Rademacher-Verteilung
BearbeitenIst Rademacher-Verteilt, und ist Exponentialverteilt zum Parameter , so ist Laplace-Verteilt zu dem Lageparameter 0 und dem Skalenparametern .
Abgrenzung zur stetigen Gleichverteilung
BearbeitenDie so definierte stetige Laplaceverteilung hat nichts mit der stetigen Gleichverteilung zu tun. Sie wird mit ihr trotzdem gerne verwechselt, weil die diskrete Gleichverteilung nach Laplace benannt ist (Laplacewürfel)
Quellen
Bearbeiten- ↑ Georgii: Stochastik. 2009, S. 225.
- ↑ Milton Abramowitz und Irene Stegun: Handbook of Mathematical Functions, 1972, S. 930