Die stetige Gleichverteilung , auch Rechteckverteilung , kontinuierliche Gleichverteilung oder Uniformverteilung genannt, ist eine stetige Wahrscheinlichkeitsverteilung . Sie hat auf einem Intervall
[
a
,
b
]
{\displaystyle [a,b]}
Wahrscheinlichkeitsdichte . Dies ist gleichbedeutend damit, dass alle Teilintervalle gleicher Länge dieselbe Wahrscheinlichkeit besitzen.
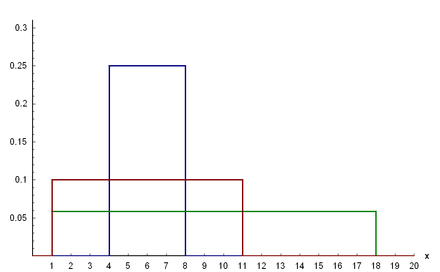
Dichtefunktion der Gleichverteilung für
a
=
4
,
b
=
8
{\displaystyle a=4,b=8}
a
=
1
,
b
=
18
{\displaystyle a=1,b=18}
a
=
1
,
b
=
11
{\displaystyle a=1,b=11}
Die Möglichkeit, die stetige Gleichverteilung auf dem Intervall von 0 bis 1 zu simulieren, bildet die Basis zur Erzeugung zahlreicher beliebig verteilter Zufallszahlen mittels der Inversionsmethode oder der Verwerfungsmethode .
Eine stetige Zufallsvariable
X
{\displaystyle X}
gleichverteilt auf dem Intervall
[
a
,
b
]
{\displaystyle [a,b]}
Dichtefunktion
f
(
x
)
{\displaystyle f(x)}
Verteilungsfunktion
F
(
x
)
{\displaystyle F(x)}
f
(
x
)
=
{
1
b
−
a
a
≤
x
≤
b
0
sonst.
=
1
12
σ
2
⋅
rect
(
x
−
μ
12
σ
2
)
{\displaystyle f(x)={\begin{cases}{\frac {1}{b-a}}&a\leq x\leq b\\0&{\text{sonst.}}\end{cases}}={\frac {1}{\sqrt {12\sigma ^{2}}}}\cdot {\text{rect}}\left({\frac {x-\mu }{\sqrt {12\sigma ^{2}}}}\right)}
F
(
x
)
=
{
0
x
≤
a
x
−
a
b
−
a
a
<
x
<
b
1
x
≥
b
{\displaystyle F(x)={\begin{cases}0&x\leq a\\{\frac {x-a}{b-a}}&a<x<b\\1&x\geq b\end{cases}}}
Als abkürzende Schreibweise für die stetige Gleichverteilung wird häufig
U
(
a
,
b
)
{\displaystyle {\mathcal {U}}(a,b)}
S
G
(
a
,
b
)
{\displaystyle {\mathcal {SG}}(a,b)}
Gleich
(
a
,
b
)
{\displaystyle {\text{Gleich}}(a,b)}
uniform
(
a
,
b
)
{\displaystyle {\text{uniform}}(a,b)}
Die Wahrscheinlichkeit, dass eine auf
[
a
,
b
]
{\displaystyle [a,b]}
X
{\displaystyle X}
[
c
,
d
]
⊆
[
a
,
b
]
{\displaystyle [c,d]\subseteq [a,b]}
P
(
c
≤
X
≤
d
)
=
F
(
d
)
−
F
(
c
)
=
d
−
c
b
−
a
{\displaystyle P(c\leq X\leq d)=F(d)-F(c)={\frac {d-c}{b-a}}}
Der Erwartungswert und der Median der stetigen Gleichverteilung sind gleich der Mitte des Intervalls
[
a
,
b
]
{\displaystyle [a,b]}
E
(
X
)
=
∫
−
∞
∞
x
f
(
x
)
d
x
=
1
b
−
a
∫
a
b
x
⋅
1
d
x
=
1
2
b
2
−
a
2
b
−
a
=
a
+
b
2
{\displaystyle \operatorname {E} (X)=\int \limits _{-\infty }^{\infty }xf(x)\,dx={\frac {1}{b-a}}\int \limits _{a}^{b}x\cdot 1\,dx={\frac {1}{2}}{\frac {b^{2}-a^{2}}{b-a}}={\frac {a+b}{2}}}
Median
(
X
)
=
F
−
1
(
1
2
)
=
a
+
b
2
{\displaystyle \operatorname {Median} (X)=F^{-1}({\tfrac {1}{2}})={\frac {a+b}{2}}}
Die Varianz der stetigen Gleichverteilung ist
Var
(
X
)
=
E
(
X
2
)
−
(
E
(
X
)
)
2
=
1
b
−
a
∫
a
b
x
2
⋅
1
d
x
−
(
a
+
b
2
)
2
=
1
3
b
3
−
a
3
b
−
a
−
(
a
+
b
2
)
2
=
1
12
(
4
b
2
+
4
a
b
+
4
a
2
−
3
a
2
−
6
a
b
−
3
b
2
)
=
1
12
(
b
−
a
)
2
.
{\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} (X^{2})-\left({\operatorname {E} (X)}\right)^{2}={\frac {1}{b-a}}\int \limits _{a}^{b}{x^{2}\cdot 1\,dx}-\left({\frac {a+b}{2}}\right)^{2}={\frac {1}{3}}{\frac {b^{3}-a^{3}}{b-a}}-\left({\frac {a+b}{2}}\right)^{2}\\&={\frac {1}{12}}\left({4b^{2}+4ab+4a^{2}-3a^{2}-6ab-3b^{2}}\right)={\frac {1}{12}}(b-a)^{2}.\end{aligned}}}
Bearbeiten
Aus der Varianz erhält man die Standardabweichung
σ
(
X
)
=
(
b
−
a
)
2
12
=
b
−
a
2
3
≈
0,289
(
b
−
a
)
{\displaystyle \sigma (X)={\sqrt {\frac {(b-a)^{2}}{12}}}={\frac {b-a}{2{\sqrt {3}}}}\approx 0{,}289(b-a)}
Die mittlere absolute Abweichung beträgt
(
b
−
a
)
/
4
{\displaystyle (b-a)/4}
Interquartilsabstand
(
b
−
a
)
/
2
{\displaystyle (b-a)/2}
einzige symmetrische Verteilung mit monotoner Dichte mit dieser Eigenschaft.
Für den Variationskoeffizienten ergibt sich:
VarK
(
X
)
=
1
3
b
−
a
a
+
b
{\displaystyle \operatorname {VarK} (X)={\frac {1}{\sqrt {3}}}{\frac {b-a}{a+b}}}
Die stetige Gleichverteilung ist symmetrisch um
a
+
b
2
{\displaystyle {\frac {a+b}{2}}}
Die Schiefe lässt sich darstellen als
v
(
X
)
=
0
{\displaystyle \operatorname {v} (X)=0}
Die Wölbung
β
2
{\displaystyle \beta _{2}}
γ
2
=
β
2
−
3
{\displaystyle \gamma _{2}=\beta _{2}-3}
β
2
=
9
5
=
1
,
8
{\displaystyle \beta _{2}={\tfrac {9}{5}}=1{,}8}
γ
2
=
−
6
5
=
−
1
,
2
{\displaystyle \gamma _{2}=-{\tfrac {6}{5}}=-1{,}2}
k
{\displaystyle k}
Moment
m
k
=
1
k
+
1
∑
i
=
0
k
a
i
b
k
−
i
=
1
k
+
1
∑
i
=
0
k
(
μ
−
3
σ
2
)
i
(
μ
+
3
σ
2
)
k
−
i
{\displaystyle m_{k}={\frac {1}{k+1}}\sum _{i=0}^{k}a^{i}b^{k-i}={\frac {1}{k+1}}\sum _{i=0}^{k}\left(\mu -{\sqrt {3\sigma ^{2}}}\right)^{i}\left(\mu +{\sqrt {3\sigma ^{2}}}\right)^{k-i}}
k
{\displaystyle k}
zentrales Moment
μ
k
=
{
(
b
−
a
)
k
2
k
(
k
+
1
)
k gerade
0
k ungerade
=
{
3
k
σ
k
(
k
+
1
)
k gerade
0
k ungerade
{\displaystyle \mu _{k}={\begin{cases}{\frac {(b-a)^{k}}{2^{k}(k+1)}}&{\text{ k gerade}}\\0&{\text{ k ungerade}}\end{cases}}={\begin{cases}{\frac {{\sqrt {3}}^{k}\sigma ^{k}}{(k+1)}}&{\text{ k gerade}}\\0&{\text{ k ungerade}}\end{cases}}}
Summe gleichverteilter Zufallsvariablen
Bearbeiten
Verteilungsdichten der Summe von bis zu 6 Gleichverteilungen U(0,1) Die Summe zweier unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt , falls die Breite der beiden Träger identisch ist. Unterscheiden sich die Trägerbreiten, so ergibt sich eine trapezförmige Verteilung. Genauer:
Zwei Zufallsvariablen seien unabhängig und stetig gleichverteilt, die eine auf dem Intervall
[
a
,
b
]
{\displaystyle [a,b]}
[
c
,
d
]
{\displaystyle [c,d]}
α
=
min
{
d
−
c
,
b
−
a
}
{\displaystyle \alpha =\min\{d-c,b-a\}}
β
=
max
{
d
−
c
,
b
−
a
}
{\displaystyle \beta =\max\{d-c,b-a\}}
Trapezverteilung :
f
:
R
→
R
,
x
⟼
{
0
x
∉
[
a
+
c
,
b
+
d
]
x
α
β
−
a
+
c
α
β
x
∈
[
a
+
c
,
a
+
c
+
α
]
1
β
x
∈
[
a
+
c
+
α
,
a
+
c
+
β
]
b
+
d
α
β
−
x
α
β
x
∈
[
a
+
c
+
β
,
b
+
d
]
{\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,x\longmapsto {\begin{cases}0&x\not \in [a+c,b+d]\\{\frac {x}{\alpha \beta }}-{\frac {a+c}{\alpha \beta }}&x\in [a+c,a+c+\alpha ]\\{\frac {1}{\beta }}&x\in [a+c+\alpha ,a+c+\beta ]\\{\frac {b+d}{\alpha \beta }}-{\frac {x}{\alpha \beta }}&x\in [a+c+\beta ,b+d]\end{cases}}}
Die Summe von unabhängigen gleichverteilten Zufallsvariablen auf dem Intervall [0;1] ist eine Irwin-Hall-Verteilung , sie nähert sich der Normalverteilung an (Zentraler Grenzwertsatz ).
Eine zuweilen verwendete Methode (Zwölferregel ) zur approximativen Erzeugung (standard-)normalverteilter Zufallszahlen funktioniert so: man summiert 12 (unabhängige) auf dem Intervall [0,1] gleichverteilte Zufallszahlen und subtrahiert 6 (das liefert die richtigen Momente, da die Varianz einer U(0,1)-verteilten Zufallsvariablen 1/12 ist und sie den Erwartungswert 1/2 besitzt).
Die charakteristische Funktion hat die Form
ϕ
X
(
t
)
=
1
(
b
−
a
)
i
t
(
e
i
t
b
−
e
i
t
a
)
=
exp
(
i
b
+
a
2
t
)
sin
(
b
−
a
2
t
)
b
−
a
2
t
{\displaystyle \phi _{X}(t)={\frac {1}{(b-a)it}}\left(e^{itb}-e^{ita}\right)=\exp \left(i{\frac {b+a}{2}}t\right){\frac {\sin \left({\frac {b-a}{2}}t\right)}{{\frac {b-a}{2}}t}}}
wobei
i
{\displaystyle i}
imaginäre Einheit darstellt.
Die momenterzeugende Funktion der stetigen Gleichverteilung ist
m
X
(
s
)
=
{
e
b
s
−
e
a
s
(
b
−
a
)
s
s
≠
0
1
s
=
0
{\displaystyle m_{X}(s)={\begin{cases}{\frac {\displaystyle e^{bs}-e^{as}}{\displaystyle (b-a)s}}&s\neq 0\\1&s=0\end{cases}}}
und speziell für
a
=
0
{\displaystyle a=0}
b
=
1
{\displaystyle b=1}
m
X
(
s
)
=
1
s
(
e
s
−
1
)
.
{\displaystyle m_{X}(s)={\frac {1}{s}}(e^{s}-1).}
Die Summe von zwei unabhängigen und stetig gleichverteilten Zufallsvariablen hat eine Dreiecksverteilung .
Sind
X
1
,
X
2
,
…
,
X
n
{\displaystyle X_{1},X_{2},\dotsc ,X_{n}}
[
0
,
1
]
{\displaystyle [0,1]}
Ordnungsstatistiken
X
(
1
)
,
X
(
2
)
,
…
,
X
(
n
)
{\displaystyle X_{(1)},X_{(2)},\dotsc ,X_{(n)}}
Betaverteilung . Genauer gilt
X
(
k
)
∼
B
(
k
,
n
−
k
+
1
)
{\displaystyle X_{(k)}\sim B(k,n-k+1)}
für
k
=
1
,
…
,
n
{\displaystyle k=1,\dotsc ,n}
Simulation von Verteilungen aus der stetigen Gleichverteilung
Bearbeiten
Mit der Inversionsmethode lassen sich gleichverteilte Zufallszahlen in andere Verteilungen überführen. Wenn
X
{\displaystyle X}
Y
=
−
1
λ
ln
(
X
)
{\displaystyle Y=-{\tfrac {1}{\lambda }}\ln(X)}
Exponentialverteilung mit dem Parameter
λ
{\displaystyle \lambda }
Bearbeiten
Die stetige Gleichverteilung lässt sich vom Intervall
[
a
,
b
]
{\displaystyle [a,b]}
Ω
{\displaystyle \Omega }
R
n
{\displaystyle \mathbb {R} ^{n}}
Lebesgue-Maß
0
<
λ
n
(
Ω
)
<
∞
{\displaystyle 0<\lambda ^{n}(\Omega )<\infty }
U
Ω
(
A
)
=
∫
A
1
λ
n
(
Ω
)
d
x
=
λ
n
(
A
)
λ
n
(
Ω
)
{\displaystyle {\mathcal {U}}_{\Omega }(A)=\int _{A}{\frac {1}{\lambda ^{n}(\Omega )}}\,dx={\frac {\lambda ^{n}(A)}{\lambda ^{n}(\Omega )}}}
für messbare
A
⊆
Ω
{\displaystyle A\subseteq \Omega }
Die Gleichverteilung ist auch auf endlichen Mengen definiert, dann heißt sie diskrete Gleichverteilung .
Häufig wird
a
=
0
{\displaystyle a=0}
b
=
1
{\displaystyle b=1}
X
∼
U
(
0
,
1
)
{\displaystyle X\sim {\mathcal {U}}(0,1)}
f
{\displaystyle f}
[
0
,
1
]
{\displaystyle [0,1]}
F
(
x
)
=
x
{\displaystyle F(x)=x}
E
(
X
)
=
1
2
{\displaystyle E(X)={\tfrac {1}{2}}}
Var
(
X
)
=
1
12
{\displaystyle \operatorname {Var} (X)={\tfrac {1}{12}}}
σ
(
X
)
=
1
12
=
1
6
3
≈
0
,
29
{\displaystyle \sigma (X)={\sqrt {\tfrac {1}{12}}}={\tfrac {1}{6}}{\sqrt {3}}\approx 0{,}29}
beliebige Intervalle
[
a
,
a
+
1
]
{\displaystyle [a,a+1]}
Summe gleichverteilter Zufallsvariablen
Ist
X
{\displaystyle X}
U
(
0
,
1
)
{\displaystyle {\mathcal {U}}(0,1)}
Y
=
(
b
−
a
)
X
+
a
{\displaystyle Y=(b-a)X+a}
U
(
a
,
b
)
{\displaystyle {\mathcal {U}}(a,b)}
Diskrete univariate Verteilungen
Kontinuierliche univariate Verteilungen
Multivariate Verteilungen
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle [c,d]\subseteq [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c4b90060cfad2522da60caeab608de43226f6e)
![{\displaystyle [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)
![{\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,x\longmapsto {\begin{cases}0&x\not \in [a+c,b+d]\\{\frac {x}{\alpha \beta }}-{\frac {a+c}{\alpha \beta }}&x\in [a+c,a+c+\alpha ]\\{\frac {1}{\beta }}&x\in [a+c+\alpha ,a+c+\beta ]\\{\frac {b+d}{\alpha \beta }}-{\frac {x}{\alpha \beta }}&x\in [a+c+\beta ,b+d]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3873fa7a21bbd83e45689defa7c5dd2cf85458bf)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle [a,a+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b53692e0b256c365ff55b9d84ac933484c3c09f6)
